Question

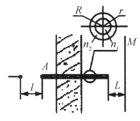
【题目】五角棱镜是光学仪器中常用的一种元件，如图所示。棱镜用玻璃制成，BC、CD两平面高度抛光，AB、DE两平面高度抛光后镀银。试证明：经BC面入射的光线，不管其方向如何，只要它能经历两次反射（在AB与DE面上），与之相应的由CD面出射的光线，必与入射光线垂直。

Answer 1

【答案】证明见解析

【解析】

如图乙所示，以i表示入射角，表示反射角，r表示折射角，次序则以下标注明。光线自透明表面的a点入射，在棱镜内反射两次，由CD面的e点出射。可以看得出，在DE面的b点：

入射角为

。

反射角为。

在四边形bEAc中，

。

而

，

于是，

在中，有

。

这就证明了：进入棱镜内的第一条光线ab总是与第三条光线ce互相垂直。

由于棱镜的C角是直角，有

。

设棱镜的折射率为n，根据折射定律有

，。

，总是成立的，而与棱镜折射率的大小及入射角的大小无关。只要光路符合上面的要求，由BC面的法线与CD面的法线垂直，又，所以出射光线总是与入射光线垂直，或者说，光线经过这种棱镜，有恒定的偏转角90°。