题目内容
如图所示,重力不计的一木板可绕O点无摩擦转动,在A端挂一正方体P,一个体重为500N的中学生站在B点时,P对水平地面的压力刚好为零,且OA=1m,OB=3m.计算:
(1)正方体P的重力;
(2)当人向O点移动的平均速度是多少米/秒时,10s后正方体对地面的压力是自身重力的三分之一.

【答案】分析:(1)中学生站在B点时,P对地面的压强刚好为零,说明绳对物体的拉力等于物体的重力,根据杠杆平衡条件F1L1=F2L2可计算物体P的重力;
(2)当人向O点移动到某点B′时,知道正方体P对地面的压力是自身重力的三分之一,而正方体对地面的压力等于P的重减去杠杆的拉力,据此求出杠杆A点受到的拉力,知道OA大小、人重,利用杠杆平衡条件求右边力臂的大小,可求人走的长度,利用速度公式求人移动的平均速度.
解答:解:
(1)当正方体对地面的压力为零时,正方体对杠杆的拉力F拉=GP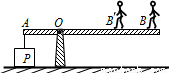
∵杠杆的平衡条件,
∴GP×OA=G人×OB
∴GP= ×G人=
×G人=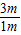 ×500N=1500N;
×500N=1500N;
(2)如图,当正方体对地面的压力为自身重力三分之一时,即F压= GP,
GP,
∵F压=GP-F拉,
∴正方体对杠杆的拉力,
F拉=GP-F压=GP-= GP=
GP= GP=
GP= ×1500N=1000N,
×1500N=1000N,
此时人位于B′点,
F拉×OA=G人×OB′,
OB′=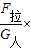 OA=
OA= ×1m=2m,
×1m=2m,
人移动的距离:
BB′=OB-OB′=3m-2m=1m,
v人= =
=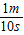 =0.1m/s.
=0.1m/s.
答:(1)正方体P的重力为1500N
(2)人向O点移动的平均速度是0.1m/s时,10s后正方体对地面的压力是自身重力的三分之一.
点评:本题考查学生对杠杆平衡条件、速度公式、力的合成的理解和运用,要求灵活运用所学知识,确定知道人走的长度是本题的关键.
(2)当人向O点移动到某点B′时,知道正方体P对地面的压力是自身重力的三分之一,而正方体对地面的压力等于P的重减去杠杆的拉力,据此求出杠杆A点受到的拉力,知道OA大小、人重,利用杠杆平衡条件求右边力臂的大小,可求人走的长度,利用速度公式求人移动的平均速度.
解答:解:
(1)当正方体对地面的压力为零时,正方体对杠杆的拉力F拉=GP

∵杠杆的平衡条件,
∴GP×OA=G人×OB
∴GP=
 ×G人=
×G人=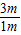 ×500N=1500N;
×500N=1500N;(2)如图,当正方体对地面的压力为自身重力三分之一时,即F压=
 GP,
GP,∵F压=GP-F拉,
∴正方体对杠杆的拉力,
F拉=GP-F压=GP-=
 GP=
GP= GP=
GP= ×1500N=1000N,
×1500N=1000N,此时人位于B′点,
F拉×OA=G人×OB′,
OB′=
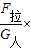 OA=
OA= ×1m=2m,
×1m=2m,人移动的距离:
BB′=OB-OB′=3m-2m=1m,
v人=
 =
=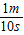 =0.1m/s.
=0.1m/s.答:(1)正方体P的重力为1500N
(2)人向O点移动的平均速度是0.1m/s时,10s后正方体对地面的压力是自身重力的三分之一.
点评:本题考查学生对杠杆平衡条件、速度公式、力的合成的理解和运用,要求灵活运用所学知识,确定知道人走的长度是本题的关键.

练习册系列答案
相关题目
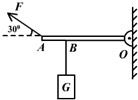 (2013?揭阳)如图所示,重力不计的杠杆OA,O为支点,在拉力F和重力为30N的重物G的作用下,杠杆OA恰在水平位置平衡.已知OA=80cm,AB=20cm,杠杆与转动轴间的摩擦忽略不计.那么拉力F的力臂L=
(2013?揭阳)如图所示,重力不计的杠杆OA,O为支点,在拉力F和重力为30N的重物G的作用下,杠杆OA恰在水平位置平衡.已知OA=80cm,AB=20cm,杠杆与转动轴间的摩擦忽略不计.那么拉力F的力臂L=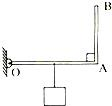 如图所示,重力不计的杠杆OAB,可绕O点在竖直平面内转动.重为100N的物体挂在OA的中点处.已知OA=40cm,AB=30cm,OA垂直于AB,杠杆与转动轴间的摩擦忽略不计.要使杠杆平衡,且OA段处于水平位置,那么作用于B端的最小力的力臂等于
如图所示,重力不计的杠杆OAB,可绕O点在竖直平面内转动.重为100N的物体挂在OA的中点处.已知OA=40cm,AB=30cm,OA垂直于AB,杠杆与转动轴间的摩擦忽略不计.要使杠杆平衡,且OA段处于水平位置,那么作用于B端的最小力的力臂等于 如图所示,重力不计的轻杆O1B和O2A,长度均为L,O1和O2为光滑的转动轴,A处有一突起物搁在O1B的中点,B处用细绳系在O2A的中点,此时两短杆便组合成一根长杆.今在O1B杆上的C点(C点为AB的中点)悬挂一个重为G的物体,则A处受到的支承力为
如图所示,重力不计的轻杆O1B和O2A,长度均为L,O1和O2为光滑的转动轴,A处有一突起物搁在O1B的中点,B处用细绳系在O2A的中点,此时两短杆便组合成一根长杆.今在O1B杆上的C点(C点为AB的中点)悬挂一个重为G的物体,则A处受到的支承力为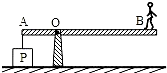 (2013?自贡)如图所示,重力不计的一木板可绕O点无摩擦转动,在A端挂一边长为50cm的正方体P,一个体重为500N的中学生站在B点时,P对地面的压强刚好为零,且OA=1m,OB=3m,则物体P的重力为
(2013?自贡)如图所示,重力不计的一木板可绕O点无摩擦转动,在A端挂一边长为50cm的正方体P,一个体重为500N的中学生站在B点时,P对地面的压强刚好为零,且OA=1m,OB=3m,则物体P的重力为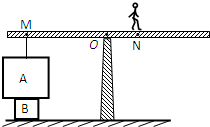 (2006?东城区二模)如图所示,重力不计的一木板可绕O点无摩擦转动,木板可以视为杠杆,在杠杆的左侧M点挂有一个边长为0.2m的立方体A,在A的下方放置一个同种材料制成的边长为0.1m的立方体B,物体B放置在水平地面上;一个人从杠杆的支点O开始以0.1m/s的速度匀速向右侧移动,经过6s后,到达N点静止,此时杠杆处于平衡状态,物体A对B的压强为7000Pa,已知MO的长度为4m.如果人从N点继续以相同的速度向右侧又经过2s后,则物体B对地面的压强为6000Pa,求:(g取10N/kg)
(2006?东城区二模)如图所示,重力不计的一木板可绕O点无摩擦转动,木板可以视为杠杆,在杠杆的左侧M点挂有一个边长为0.2m的立方体A,在A的下方放置一个同种材料制成的边长为0.1m的立方体B,物体B放置在水平地面上;一个人从杠杆的支点O开始以0.1m/s的速度匀速向右侧移动,经过6s后,到达N点静止,此时杠杆处于平衡状态,物体A对B的压强为7000Pa,已知MO的长度为4m.如果人从N点继续以相同的速度向右侧又经过2s后,则物体B对地面的压强为6000Pa,求:(g取10N/kg)