题目内容
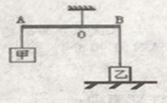
【题目】如图所示,水平桌面上放有甲、乙、丙、丁四个完全相同的圆柱形容器。其中甲容器内只有水;乙容器内有木块漂浮在水面上;丙容器内有一个装有铝块的平底塑料盒漂浮在水面上,塑料盒底始终与容器底平行,且塑料盒的底面积等于圆柱形容器底面积的一半;丁容器中用细线悬吊着一个实心的铝球浸没在水中。已知四个容器中的水面一样高, ![]() 水=0.6×103kg/m3;
水=0.6×103kg/m3; ![]() 酒精=0.8×103kg/m3;
酒精=0.8×103kg/m3; ![]() 铝=2.7×103kg/m3,对于这一情景,有如下一些说法。这些说法中正确的是( )
铝=2.7×103kg/m3,对于这一情景,有如下一些说法。这些说法中正确的是( )

A. 各容器对水平桌面的压强不同
B. 向乙容器中倒入酒精后,木块底部受到的压强将增大
C. 将塑料盒内的铝块取出放到水平桌面上,塑料盒底距容器底的距离的增大值等于水面下降高度的数值
D. 将悬吊铝球的细线剪断后,丁容器对水平桌面压力的增大值等于铝球所受重力的大小
【答案】C
【解析】A∵木块漂浮,∴木块受到的浮力等于木块重,∵F浮=ρ水V排g,∴木块受到的重力等于排开的水重,∵甲、乙容器水面等高,∴乙容器的总重等于甲容器的总重,∵G=mg,∴乙容器的总质量与甲容器的总质量相同,则甲乙对桌面的压力相等;同理可以得出,丙容器的总质量与甲容器的总质量相同,则甲丙对桌面的压力相等;丁容器中水重力的增加的量等于小球排开液体的重力,因液面与甲容器的相平,所以甲丁对桌面的压力相等;因四个容器底面积相同,由p=![]() 可知它们的压强相同,故A错误;B.乙容器中再倒入酒精后,使水的密度减小,但木块还是漂浮,受到的浮力相等,∵F浮=ρ水V排g,∴排开水的体积增大,使木块在液面下的体积增大,因F浮=pS木块底,木块的底面积不变,所以木块底部受到的压强不变,故B错误;C.铝块在塑料盒内处于漂浮,F浮=G盒+G铝,将塑料盒内的铝块取出后,F浮′=G盒,△F浮=F浮
可知它们的压强相同,故A错误;B.乙容器中再倒入酒精后,使水的密度减小,但木块还是漂浮,受到的浮力相等,∵F浮=ρ水V排g,∴排开水的体积增大,使木块在液面下的体积增大,因F浮=pS木块底,木块的底面积不变,所以木块底部受到的压强不变,故B错误;C.铝块在塑料盒内处于漂浮,F浮=G盒+G铝,将塑料盒内的铝块取出后,F浮′=G盒,△F浮=F浮![]() F浮′=G盒
F浮′=G盒![]() G铝-G盒=G铝,根据阿基米德原理可知排开水的体积△V=V排
G铝-G盒=G铝,根据阿基米德原理可知排开水的体积△V=V排![]() V排′=
V排′=![]() ,∴根据V=Sh可知水面下降高度为:△h=
,∴根据V=Sh可知水面下降高度为:△h=![]() ,由于塑料盒受到的浮力减小,塑料盒上浮,则根据△F浮=△pS得:△F浮=△pS=pS盒-p′S盒=ρ水ghS盒
,由于塑料盒受到的浮力减小,塑料盒上浮,则根据△F浮=△pS得:△F浮=△pS=pS盒-p′S盒=ρ水ghS盒![]() ρ水gh′S盒=△hρ水gS盒,∴△h′=
ρ水gh′S盒=△hρ水gS盒,∴△h′=![]() ,∵容器的水面下降,∴塑料盒底距容器底的距离的增大值为:△h″=△h′
,∵容器的水面下降,∴塑料盒底距容器底的距离的增大值为:△h″=△h′![]() △h=
△h=![]() (
(![]() ),∵塑料盒的底面积等于圆柱形容器底面积的一半;即S盒=
),∵塑料盒的底面积等于圆柱形容器底面积的一半;即S盒=![]() S容器,则
S容器,则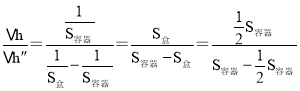 =1,∴△h″=△h,即塑料盒底距容器底的距离的增大值等于水面下降高度的数值,故C正确;D∵细线剪断前,桌面受到的压力等于容器与水的重力、小球排开液体的重力之和,将悬吊铝球的细线剪断后,桌面受到的压力等于容器与水的重力、铝球对容器底部的压力之和,而铝球对容器底部的压力等于铝球的重力减去受到的浮力,根据阿基米德原理可知铝球受到的浮力等于小球排开液体的重力,所以容器对水平桌面压力的增大值等于铝球所受重力减去受到的浮力,故D错误;故选C.
=1,∴△h″=△h,即塑料盒底距容器底的距离的增大值等于水面下降高度的数值,故C正确;D∵细线剪断前,桌面受到的压力等于容器与水的重力、小球排开液体的重力之和,将悬吊铝球的细线剪断后,桌面受到的压力等于容器与水的重力、铝球对容器底部的压力之和,而铝球对容器底部的压力等于铝球的重力减去受到的浮力,根据阿基米德原理可知铝球受到的浮力等于小球排开液体的重力,所以容器对水平桌面压力的增大值等于铝球所受重力减去受到的浮力,故D错误;故选C.

 名校课堂系列答案
名校课堂系列答案