Question

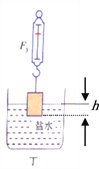
【题目】用一根不可伸长的轻绳，将一体积为V的长方体木块系于底面积为S0的圆柱形薄壁容器底部。往容器中缓慢注入密度为ρ0的液体，当木块露出液面的体积与浸入水中的体积之比为1：4时，绳子受到的拉力是木块重力的，如图所示。若将木块露出水面的部分切除，绳子刚好被拉断。求：

（1）木块的密度；

（2）细线刚好被拉断时与细线断后容器中液面恢复稳定时，容器底部所受液体压强的变化量。

Answer 1

【答案】（1）ρ0；（2）

【解析】

（1）已知木块体积（排开水的体积），利用阿基米德原理求所受浮力，根据已知得出拉力与重力的关系；根据物体受力平衡条件即可求解。

（2）将木块露出水面的部分切除，细线刚好被拉断时，木块受到重力、浮力和细线的拉力，其关系式为F浮＝G+F；细线断后容器中液面恢复稳定时，木块漂浮，F浮′＝G′；将二式联立，根据阿基米德原理和压强计算公式，得出容器底部所受液体压强的变化量。

（1）由于木块露出液面的体积与浸入水中的体积之比为1：4，即：V露：V排＝1：4，

由于V露+V排＝V，所以，V排＝V，

受到的浮力为：F浮＝ρ0gV排＝ρ0gV，

G＝mg＝ρ木Vg；

绳子受到的拉力F＝G＝ρ木Vg；

由于木块在绳子的拉力作用下处于静止；

则F浮＝F+G，

即：ρ0gV＝ρ木Vg+ρ木Vg，

解得：ρ木＝ρ0，

（2）由于将木块露出水面的部分切除，则剩余木块的重力为G′

＝G＝×ρ木Vg＝×ρ0Vg＝ρ0Vg；

细线刚好被拉断时，即木块处于浸没状态时，F浮＝G+F＝G+G＝G＝×ρ木Vg＝×ρ0Vg＝ρ0Vg；

液面恢复稳定后，F浮′＝G′＝ρ0Vg；

则：△F浮＝F浮﹣F浮′＝ρ0Vg﹣ρ0Vg＝ρ0Vg，

结合阿基米德原理可得：ρ0g（V排﹣V排′）＝ρ0Vg，

即：ρ0g△h′S0＝ρ0Vg﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣①，

而液体压强的变化量：△p＝ρ0g△h′﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣②

由①②可得：△p＝=。