题目内容
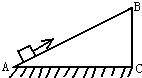如图所示，一个重为50N的物体，在F=10N的拉力作用下，自底端A匀速运动到顶点B所需的时间是5s，斜面高为1.5m，机械效率为75%，求物体从底端A运动到顶点B的速度和物体受到的摩擦力．分析：（1）将重物提升1.5m做的功为有用功，利用W=Gh求有用功；知道机械效率，利用效率公式求总功；知道拉力大小，利用W总=Fs求斜面长；又知道运动时间，再利用速度公式求物体从A运动到顶点B的速度；
（2）根据W总=W有用-W额求出克服摩擦力做的额外功，然后根据公式W额=fs求出摩擦力的大小．
（2）根据W总=W有用-W额求出克服摩擦力做的额外功，然后根据公式W额=fs求出摩擦力的大小．
解答：已知：物体重力G=50N，拉力F=10N，时间t=5s，斜面高为h=1.5m，机械效率为η=75%
求：物体的运动速度v=？；物体受到的摩擦力f=？
解：（1）克服重力做的有用功：
W有用=Gh=50N×1.5m=75J；
∵η=
，
∴拉力做的总功：
W总=
=
=100J，
∵W总=Fs，
∴斜面长：
s=
=
=10m，
物体的运动速度：
v=
=
=2m/s；
（2）∵W总=W有用-W额
∴克服摩擦力做的额外功：
W额=W总-W有用=100J-75J=25J，
∵W额=fs
∴物体受到的摩擦力：
f=
=
=2.5N．
答：物体从底端A运动到顶点B的速度是2m/s；
物体受到的摩擦力为2.5N．
求：物体的运动速度v=？；物体受到的摩擦力f=？
解：（1）克服重力做的有用功：
W有用=Gh=50N×1.5m=75J；
∵η=
| W有用 |
| W总 |
∴拉力做的总功：
W总=
| W有用 |
| η |
| 75J |
| 75% |
∵W总=Fs，
∴斜面长：
s=
| W总 |
| F |
| 100J |
| 10N |
物体的运动速度：
v=
| s |
| t |
| 10m |
| 5s |
（2）∵W总=W有用-W额
∴克服摩擦力做的额外功：
W额=W总-W有用=100J-75J=25J，
∵W额=fs
∴物体受到的摩擦力：
f=
| W额 |
| s |
| 25J |
| 10m |
答：物体从底端A运动到顶点B的速度是2m/s；
物体受到的摩擦力为2.5N．
点评：本题考查了使用斜面时有用功、总功、额外功、机械效率的计算方法，知道将重物提升1.5m做的功为有用功、沿斜面推力做的功为总功、克服摩擦力做的功是额外功是解决本题的关键．
练习册系列答案
相关题目
如图所示装置，重为GM=100N的物体M放置在水平桌面上，两侧用水平细线拴住，左侧水平细线通过定滑轮悬挂重为GA=80N的物体A，A浸没在一个足够大的盛水容器中，右侧通过滑轮组拉着重为GB=150N的物体B，恰好使物体M在水平桌面上匀速向右运动（物体A未露出水面）；撤去盛水容器，用一个竖直向下的力F1拉物体A，使物体B匀速上升时，滑轮组的机械效率为η1；当把盛水容器放在右侧使物体B浸没在水中，此时在再用一个竖直向下的力F2拉物体A，使物体B在5s内匀速上升10cm（物体B未露出水面）时，滑轮组的机械效率为η2；已知物体A、B和水的密度之比为ρA：ρB：ρ水=2：5：1，两次拉力之比为F1：F2=3：2．若不计绳重、滑轮组装置的摩擦及物体A、B在水中的阻力，g取10N/kg．求：
如图所示，一个重为50牛的物体，在F=10牛外力作用下，自底端A匀速运动到B所需时间8秒，斜高为1.5米，机械效率为75%，求物体从A运动到顶点B的速度为多少？
如图所示，一个重为50牛的物体，在F=10牛外力作用下，自底端A匀速运动到B所需时间8秒，斜高为1.5米，机械效率为75%，求物体从A运动到顶点B的速度为多少？
