题目内容
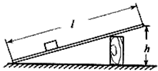
 如图是某同学探究“斜面的机械效率”实验装置图.实验前他做了如下猜想:
如图是某同学探究“斜面的机械效率”实验装置图.实验前他做了如下猜想:A.斜面的机械效率可能与斜面的粗糙程度有关.
B.斜面的机械效率可能与斜面的倾斜程度有关.
他在实验时用弹簧测力计拉着同一木块沿斜面向上做匀速直线运动,分别做了四次实验,并记录实验数据如下:
| 实验 次数 |
斜面倾 斜程度 |
斜面粗糙程度 | 木块重量G/N | 斜面高h/m | 拉力 F/N |
斜面长 s/m |
克服重力 做功W1/J |
拉力做 功W2/J |
机械 效率η |
| 1 | 较缓 | 木板表面 | 2 | 0.1 | 0.6 | 0.5 | 0.2 | 0.3 | 67% |
| 2 | 较陡 | 木板表面 | 2 | 0.2 | 1 | 0.5 | 0.4 | 0.5 | 80% |
| 3 | 最陡 | 木板表面 | 2 | 0.3 | 1.4 | 0.5 | 0.6 | 0.7 | 86% |
| 4 | 最陡 | 毛巾表面 | 2 | 0.3 | 1.6 | 0.5 | (a) | (b) | (c) |
0.6
0.6
,(b)0.8
0.8
,(c)75
75
,(2)比较第四列和第六列两次实验数据可知:使用斜面
省力
省力
,比较第八列和第九列两次实验数据可知:使用斜面不省功
不省功
(3)比较1、2、3次实验得到的结论是:当斜面粗糙程度相同时,斜面越陡机械效率
高
高
(4)比较2、4次实验
不能
不能
(能/不能)得到斜面的机械效率与斜面的粗糙程度有关,理由是没有控制斜面的倾斜程度相同
没有控制斜面的倾斜程度相同
.分析:(1)根据表中实验数据,应用功的计算公式求出功、斜面的效率.
(2)分析表中实验数据,根据实验数据得出结论.
(3)分析表中实验数据,根据实验控制的变量与实验数据得出实验结论.
(4)探究斜面机械效率与斜面粗糙程度的关系,应控制斜面的粗糙程度、物体重力都相同.
(2)分析表中实验数据,根据实验数据得出结论.
(3)分析表中实验数据,根据实验控制的变量与实验数据得出实验结论.
(4)探究斜面机械效率与斜面粗糙程度的关系,应控制斜面的粗糙程度、物体重力都相同.
解答:解:(1)由表中实验数据可知,克服重力做功W1=Gh=2N×0.3m=0.6J,拉力做功W2=Fs=1.6N×0.5m=0.8J,
斜面的效率η=
×100%=
×100%=75%.
(2)由表中第四列和第六列两次实验数据可知,拉力小于木块重力,由此可得:使用斜面省力;由表中第八列和第九列两次实验数据可知,拉力的功大于克服重力的功,由此可知:使用斜面不省功.
(3)由表中实验序号为1、2、3的实验数据可知,当斜面粗糙程度相同时,斜面越陡机械效率高.
(4)由表中实验序号为2、4的实验数据可知,实验没有控制斜面的倾斜程度相同,不能得到斜面的机械效率与斜面的粗糙程度有关.
故答案为:(1)0.6;0.8;75;(2)省力;不省功;(3)高;(4)不能;没有控制斜面的倾斜程度相同.
斜面的效率η=
| W1 |
| W2 |
| 0.6J |
| 0.8J |
(2)由表中第四列和第六列两次实验数据可知,拉力小于木块重力,由此可得:使用斜面省力;由表中第八列和第九列两次实验数据可知,拉力的功大于克服重力的功,由此可知:使用斜面不省功.
(3)由表中实验序号为1、2、3的实验数据可知,当斜面粗糙程度相同时,斜面越陡机械效率高.
(4)由表中实验序号为2、4的实验数据可知,实验没有控制斜面的倾斜程度相同,不能得到斜面的机械效率与斜面的粗糙程度有关.
故答案为:(1)0.6;0.8;75;(2)省力;不省功;(3)高;(4)不能;没有控制斜面的倾斜程度相同.
点评:本题考查了实验数据计算、实验数据分析、应用功的计算公式、效率公式、应用控制变量法分析表中实验数据即可正确解题.

练习册系列答案
相关题目
 某物理学习小组,针对同学中存在的有关斜面问题的一些疑惑,进行了实验探究和理论探究活动.
某物理学习小组,针对同学中存在的有关斜面问题的一些疑惑,进行了实验探究和理论探究活动.[实验探究]
将长度为 1m的长木板的一端垫高,构成长度一定高度可调的斜面(如图所示).用沿斜面向上的拉力F使重为10N的滑块沿斜面匀速向上运动.完成斜面机械效率测量.表呈现的是部分实验数据:
| 实验次数 | 1 | 2 | 3 | 4 |
| 斜面高度h/m | 0.15 | 0.20 | 0.25 | 0.30 |
| 拉力F/N | 2.7 | 3.2 | 3.6 | 4.1 |
| 机械效率η | 0.56 | 0.63 | 0.69 | 0.73 |
请报据表3中的实验数据,写出正确的结论.
(2)疑惑二,“斜面倾斜程度越大拉力越大,滑块受到的摩擦力也一定越大吗?”
请进一步分析表3实验数据,写出正确的结论:
简述理由:
[理论探究]
(3)疑惑三.“滑块受到的摩擦力是一个‘不可直接测量’量,能通过‘可测量’量求出摩擦力吗?”
请根据已有的知识推导:对于倾斜程度不同的斜面,在拉力F作用下(拉力方向沿斜面向上)使重为G的滑块沿斜面匀速移动时,滑块受到的摩擦力f的数学表达式(斜面的长L和斜面的高h均为“可测量”量)

 (2010?黄石模拟)某物理学习小组,针对同学中存在的有关斜面问题的一些疑惑,进行了实验探究和理论探究活动.
(2010?黄石模拟)某物理学习小组,针对同学中存在的有关斜面问题的一些疑惑,进行了实验探究和理论探究活动. (2010?介休市二模)某同学为探究斜面的机械效率,做了如下实验:如图所示,物体G所受到的重力大小为40N.
(2010?介休市二模)某同学为探究斜面的机械效率,做了如下实验:如图所示,物体G所受到的重力大小为40N. 在探究“杠杆的平衡条件”的实验中,某同学记录了三次实验数据如下表:
在探究“杠杆的平衡条件”的实验中,某同学记录了三次实验数据如下表: