题目内容
用不等臂天平称质量为4g的物体,先放在右盘中称,再放左盘中称,记下两次的结果,则其记录值可能为
- A.2g,5g
- B.4g,1g
- C.8g,2g
- D.3.2g,6g
C
分析:天平是利用杠杆的平衡条件制成的,两次称量,杠杆两次平衡,由此可以得到两个杠杆的平衡方程,由此入手解决此题.
解答:不等臂杠杆的结构图所示.
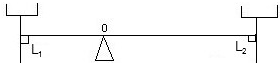
当将物体放在天平的左盘时,天平处于平衡状态,设此时右盘中砝码的质量为m1,根据杠杆的平衡条件可得:4L1=m1L2①
当将物体放在天平的右盘时,天平处于平衡状态,设此时左盘中砝码的质量为m2,根据杠杆的平衡条件可得:4L2=m2L1 ②
整理①式得: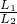 =
=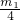 ③
③
整理②式得: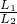 =
= ④
④
联立③④得: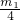 =
= 即:m1m2=16
即:m1m2=16
由此可得两次记录值可能为:8g,2g.
综上分析故选C.
点评:将两次称量与两次利用杠杆的平衡条件相对应是解决此题的关键,明确在两次杠杆的平衡中,两个力臂的比值不变是解决此题的突破口.
分析:天平是利用杠杆的平衡条件制成的,两次称量,杠杆两次平衡,由此可以得到两个杠杆的平衡方程,由此入手解决此题.
解答:不等臂杠杆的结构图所示.

当将物体放在天平的左盘时,天平处于平衡状态,设此时右盘中砝码的质量为m1,根据杠杆的平衡条件可得:4L1=m1L2①
当将物体放在天平的右盘时,天平处于平衡状态,设此时左盘中砝码的质量为m2,根据杠杆的平衡条件可得:4L2=m2L1 ②
整理①式得:
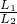 =
=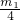 ③
③整理②式得:
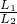 =
= ④
④联立③④得:
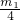 =
= 即:m1m2=16
即:m1m2=16由此可得两次记录值可能为:8g,2g.
综上分析故选C.
点评:将两次称量与两次利用杠杆的平衡条件相对应是解决此题的关键,明确在两次杠杆的平衡中,两个力臂的比值不变是解决此题的突破口.

练习册系列答案
相关题目