题目内容
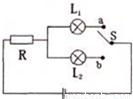
如如图所示电路.电源电压不变,L1标有“4V 2W”,L2标有“8V 4W”.当开关S接a时.L1恰好正常发光,当开关S接b时.L2两端电压为6.4V.(忽略温度变化对电阻的影响)求:(1)开关S接b时L2实际功率;
(2)开关S接a时电阻R在30s内所产生的热量.
【答案】分析:(1)已知L2灯的额定电压及额定功率,则由额定功率利用功率公式可求得L2灯的电阻,再由功率公式P= 可求 得实际功率;
可求 得实际功率;
(2)开关接a时,灯L1正常发光,则由功率公式可求得灯泡L1的阻值及电路中的电流;因电源电压不变,由欧姆定律得出两种情况下的电压表达式,联立可解得R阻值,由焦耳定律可求得30s内所产生的热量.
解答:解:(1)开关S接b时,R与L2串联
L2灯的电阻:R2=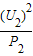 =
=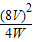 =16Ω;
=16Ω;
L2实际功率P2实=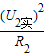 =
=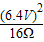 =2.56W;
=2.56W;
(2)开关S接a时,R与L1串联,且L1恰好正常发光
R1=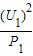 =
=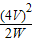 =8Ω,
=8Ω,
I1=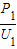 =
=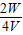 =0.5A;
=0.5A;
由I1(R+R1)=I2(R+R2)
可得R=24Ω
∴电阻R在30s内所产生的热量:
Q=(I1)2Rt=(0.5A)2×24Ω×30s=180J.
答:(1)L2实际功率为2.56W;(2)电阻R产生的热量为180J.
点评:在纯电阻电路中功率P=UI=I2R=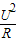 ,可选用的公式较多,故应仔细分析题意,由题目中的已知量灵活选择合适的公式求解.
,可选用的公式较多,故应仔细分析题意,由题目中的已知量灵活选择合适的公式求解.
 可求 得实际功率;
可求 得实际功率;(2)开关接a时,灯L1正常发光,则由功率公式可求得灯泡L1的阻值及电路中的电流;因电源电压不变,由欧姆定律得出两种情况下的电压表达式,联立可解得R阻值,由焦耳定律可求得30s内所产生的热量.
解答:解:(1)开关S接b时,R与L2串联
L2灯的电阻:R2=
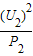 =
=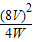 =16Ω;
=16Ω;L2实际功率P2实=
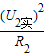 =
=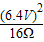 =2.56W;
=2.56W;(2)开关S接a时,R与L1串联,且L1恰好正常发光
R1=
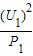 =
=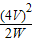 =8Ω,
=8Ω,I1=
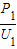 =
=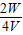 =0.5A;
=0.5A;由I1(R+R1)=I2(R+R2)
可得R=24Ω
∴电阻R在30s内所产生的热量:
Q=(I1)2Rt=(0.5A)2×24Ω×30s=180J.
答:(1)L2实际功率为2.56W;(2)电阻R产生的热量为180J.
点评:在纯电阻电路中功率P=UI=I2R=
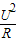 ,可选用的公式较多,故应仔细分析题意,由题目中的已知量灵活选择合适的公式求解.
,可选用的公式较多,故应仔细分析题意,由题目中的已知量灵活选择合适的公式求解. 
练习册系列答案
相关题目
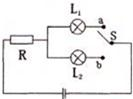 如如图所示电路.电源电压不变,L1标有“4V 2W”,L2标有“8V 4W”.当开关S接a时.L1恰好正常发光,当开关S接b时.L2两端电压为6.4V.(忽略温度变化对电阻的影响)
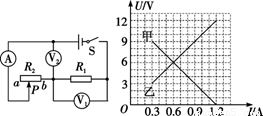
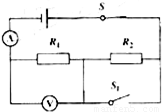
如如图所示电路.电源电压不变,L1标有“4V 2W”,L2标有“8V 4W”.当开关S接a时.L1恰好正常发光,当开关S接b时.L2两端电压为6.4V.(忽略温度变化对电阻的影响)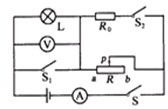 如图所示电路,电源电压不变,灯泡L标有“6V 0.5A”字样.当S闭合,S1、S2断开,滑片P从b端滑到中点时,电流表的示数变化了0.1A,此时电压表的示数为6V;保持滑片P的位置不变,闭合S1、S2,电流表的示数又变化了2A;(不考虑温度对灯泡电阻的影响).
如图所示电路,电源电压不变,灯泡L标有“6V 0.5A”字样.当S闭合,S1、S2断开,滑片P从b端滑到中点时,电流表的示数变化了0.1A,此时电压表的示数为6V;保持滑片P的位置不变,闭合S1、S2,电流表的示数又变化了2A;(不考虑温度对灯泡电阻的影响).