题目内容
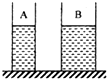如图所示，两个盛有等高液体的圆柱形容器A和B，底面积不同（SA＜SB），液体对容器底部的压力相等，现将甲球浸没在A容器的液体中，乙球浸没在B容器的液体中，容器中均无液体溢出，若此时液体对各自容器底部的压强相等，则一定是（ ）分析：液体对容器底部的压力相等，根据压强公式知道两容器里的液体对容器底部的压强的大小关系；进一步求出液体的密度关系；知道液体对容器底的压强相等得出排开液体体积的关系和排开液体重力的关系，结合体积公式和阿基米德原理即可判断出两球体积的关系和两球受到浮力的关系．
解答：解：因为两种液体对容器底部的压力相等，并且SA＜SB，根据公式p=
可知，A内液体对容器底部产生的压强大；从图中可知，两液体高度相等，由p=ρgh可知，A内液体的密度大；
放入金属球后，两种液体对容器底部的压强相等，根据公式P=ρgh可知，B内液体升高的高度大，由V=Sh可知，乙的体积大于甲的体积；由于无法判断两球的密度关系，所以也无法判断两球的质量关系；故B正确，AC错误；
放入金属球后，两种液体对容器底部的压强相等，并且原来A内液体对容器底部产生的压强大，SA＜SB，根据公式p=
可知，乙球排开液体的重力大于甲球排开液体的重力，甲球的浮力小于乙球．
故选BD．
| F |
| S |
放入金属球后，两种液体对容器底部的压强相等，根据公式P=ρgh可知，B内液体升高的高度大，由V=Sh可知，乙的体积大于甲的体积；由于无法判断两球的密度关系，所以也无法判断两球的质量关系；故B正确，AC错误；
放入金属球后，两种液体对容器底部的压强相等，并且原来A内液体对容器底部产生的压强大，SA＜SB，根据公式p=
| △F |
| S |
故选BD．
点评：本题考查压强、压力、阿基米德等的有关问题，对圆柱形直壁容器，知道液体对容器底的压力F=ps=ρghs=ρvg=mg是本题的关键．
练习册系列答案
相关题目
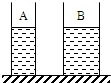（2010?上海）如图所示，两个盛有等高液体的圆柱形容器A和B，底面积不同（SA＜SB），液体对容器底部的压强相等，现将甲球浸没在A容器的液体中，乙球浸没在B容器的液体中，容器中均无液体溢出，若此时液体对各自容器底部的压力相等，则一定是（ ）
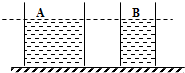（2012?黄浦区一模）如图所示，两个盛有等高液体的圆柱形容器A和B，底面积不同（SA＞SB），液体对容器底部的压强相等．现将甲球浸没在A容器的液体中，乙球浸没在B容器的液体中，容器中均无液体溢出，若此时液体对各自容器底部的压力相等，则一定是（ ）
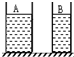如图所示，两个盛有等高液体的圆柱形容器A和B，底面积不同（SA＞SB），液体对容器底部的压力相等．下列分析正确的是（ ）
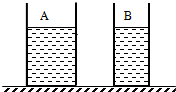（2011?宝山区一模）如图所示，两个盛有等高液体的圆柱形容器A和B，底面积不同（SA＞SB），液体对容器底部的压强相等．现将甲球浸没在A容器的液体中，乙球浸没在B容器的液体中，容器中均无液体溢出，若此时液体对各自容器底部的压力相等，则一定（ ）