题目内容
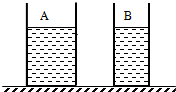 (2011?宝山区一模)如图所示,两个盛有等高液体的圆柱形容器A和B,底面积不同(SA>SB),液体对容器底部的压强相等.现将甲球浸没在A容器的液体中,乙球浸没在B容器的液体中,容器中均无液体溢出,若此时液体对各自容器底部的压力相等,则一定( )
(2011?宝山区一模)如图所示,两个盛有等高液体的圆柱形容器A和B,底面积不同(SA>SB),液体对容器底部的压强相等.现将甲球浸没在A容器的液体中,乙球浸没在B容器的液体中,容器中均无液体溢出,若此时液体对各自容器底部的压力相等,则一定( )分析:(1)液体对容器底部的压强相等,SA>SB,根据F=PS,可判断容器A和B底部受的压力大小,因为容器A和B是圆柱形,底部受的压力等于液体重力.可判断出两容器液体重力大小.
甲球浸没在A容器的液体中,乙球浸没在B容器的液体中,液体对各自容器底部的压力相等,若漂浮或悬浮液体对各自容器底部的压力等于液体重力与球重力之和,可判断两球的质量和重力大小.若下沉液体对各自容器底部的压力小于液体重力与球重力之和.
(2)因为放入球之前,容器A和B液相平,液体对容器底部的压强相等,根据P=ρgh可知,液体密度相等.放入球后,压力F=PS=ρghS,又压力相等,所以hS相等,即两容器液体体积与球的体积之和相等.又因为因为放入球之前,容器A和B液相平,SA>SB可知A容器中液体体积大于B容器中液体体积.即可判断两球体积大小;
又因两球浸没有液体中,根据阿基米德定律可判断浮力大小.
甲球浸没在A容器的液体中,乙球浸没在B容器的液体中,液体对各自容器底部的压力相等,若漂浮或悬浮液体对各自容器底部的压力等于液体重力与球重力之和,可判断两球的质量和重力大小.若下沉液体对各自容器底部的压力小于液体重力与球重力之和.
(2)因为放入球之前,容器A和B液相平,液体对容器底部的压强相等,根据P=ρgh可知,液体密度相等.放入球后,压力F=PS=ρghS,又压力相等,所以hS相等,即两容器液体体积与球的体积之和相等.又因为因为放入球之前,容器A和B液相平,SA>SB可知A容器中液体体积大于B容器中液体体积.即可判断两球体积大小;
又因两球浸没有液体中,根据阿基米德定律可判断浮力大小.
解答:解:(1)液体对容器底部的压强相等,SA>SB,
GA=FA=PSA,GB=FB=PSB,
可见GA>GB,
放入小球后,若小球漂浮或悬浮,液体对各自容器底部的压力相等,
GA+G甲=GB+G乙,因为,GA>GB,
所以,G甲<G乙,甲的质量也小于乙的质量.
若小球下沉,液体对容器A底部的压力:FA′<GA+G甲,
液体对容器A底部的压力:FB′<GB+G乙,
虽然液体对各自容器底部的压力相等,但是,GA+G甲与GB+G乙的关系不能确定.即G甲与G乙的关系也不能确定.
故AB错误.
(2)因为放入球之前,容器A和B液相平,液体对容器底部的压强相等,
根据P=ρgh可知,ρA=ρB,
放入球后,FA=ρAghASA,FB=ρBghBSB,
又压力相等,所以hASA=hBSB,
即两容器液体体积与球的体积之和相等.
又因为,放入球之前,A容器液体体积大于B容器液体体积.
所以,甲球的体积小于乙球的体积,
故C错误.
(3)根据阿基米德定律,两种液体密度相同,甲球和乙球都浸没在液体中,甲球的体积小于乙球的体积,
所以,甲球所受浮力小于乙球所受浮力,故D正确.
故选D.
GA=FA=PSA,GB=FB=PSB,
可见GA>GB,
放入小球后,若小球漂浮或悬浮,液体对各自容器底部的压力相等,
GA+G甲=GB+G乙,因为,GA>GB,
所以,G甲<G乙,甲的质量也小于乙的质量.
若小球下沉,液体对容器A底部的压力:FA′<GA+G甲,
液体对容器A底部的压力:FB′<GB+G乙,
虽然液体对各自容器底部的压力相等,但是,GA+G甲与GB+G乙的关系不能确定.即G甲与G乙的关系也不能确定.
故AB错误.
(2)因为放入球之前,容器A和B液相平,液体对容器底部的压强相等,
根据P=ρgh可知,ρA=ρB,
放入球后,FA=ρAghASA,FB=ρBghBSB,
又压力相等,所以hASA=hBSB,
即两容器液体体积与球的体积之和相等.
又因为,放入球之前,A容器液体体积大于B容器液体体积.
所以,甲球的体积小于乙球的体积,
故C错误.
(3)根据阿基米德定律,两种液体密度相同,甲球和乙球都浸没在液体中,甲球的体积小于乙球的体积,
所以,甲球所受浮力小于乙球所受浮力,故D正确.
故选D.
点评:(1)本题考查了液体压强的计算及压强公式的运用,难度较大.
(2)要判断B选项,需要分情况讨论,然后找出圆柱形容器底部受到液体的压力与容器内物体的重力的关系,再做出判断.
(3)要判断CD选项,hASA=hBSB,即放入球后,球和液体的总体积相等是关键.
(2)要判断B选项,需要分情况讨论,然后找出圆柱形容器底部受到液体的压力与容器内物体的重力的关系,再做出判断.
(3)要判断CD选项,hASA=hBSB,即放入球后,球和液体的总体积相等是关键.

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
 (2011?宝山区一模)为了探究浮力的有关规律,用测力计、物体A、两个相同的容器、酒精和盐水等进行实验.实验中,先将物体A挂在已调好的测力计下,且处于静止状态,如图(a)所示.接着将物体A分别浸入酒精和盐水中静止不动,实验过程如图(b)和(c)所示.请仔细观察图中的测力计示数,归纳得出初步结论.(已知酒精的密度小于盐水的密度.)
(2011?宝山区一模)为了探究浮力的有关规律,用测力计、物体A、两个相同的容器、酒精和盐水等进行实验.实验中,先将物体A挂在已调好的测力计下,且处于静止状态,如图(a)所示.接着将物体A分别浸入酒精和盐水中静止不动,实验过程如图(b)和(c)所示.请仔细观察图中的测力计示数,归纳得出初步结论.(已知酒精的密度小于盐水的密度.)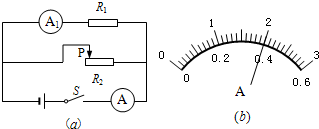 (2011?宝山区一模)在图(a)所示的电路中,电源电压为4伏且不变,电阻R1为20欧.当滑动变阻器R2上的滑片P移至某处,闭合电键S,电路中电流表A的示数如图(b)所示.求:
(2011?宝山区一模)在图(a)所示的电路中,电源电压为4伏且不变,电阻R1为20欧.当滑动变阻器R2上的滑片P移至某处,闭合电键S,电路中电流表A的示数如图(b)所示.求: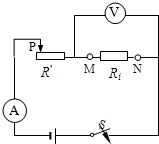 (2011?宝山区一模)某实验小组用图所示的电路,探究导体“通过导体的电流与导体电阻的关系”,他们分别将三个定值电阻Ri先后逐个接在图14中的M、N两端,且电源电压始终保持不变.
(2011?宝山区一模)某实验小组用图所示的电路,探究导体“通过导体的电流与导体电阻的关系”,他们分别将三个定值电阻Ri先后逐个接在图14中的M、N两端,且电源电压始终保持不变.