题目内容
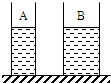 (2010?上海)如图所示,两个盛有等高液体的圆柱形容器A和B,底面积不同(SA<SB),液体对容器底部的压强相等,现将甲球浸没在A容器的液体中,乙球浸没在B容器的液体中,容器中均无液体溢出,若此时液体对各自容器底部的压力相等,则一定是( )
(2010?上海)如图所示,两个盛有等高液体的圆柱形容器A和B,底面积不同(SA<SB),液体对容器底部的压强相等,现将甲球浸没在A容器的液体中,乙球浸没在B容器的液体中,容器中均无液体溢出,若此时液体对各自容器底部的压力相等,则一定是( )分析:知道液体深度相同、液体对容器底部的压强相等,根据液体压强公式知道两容器里的液体密度相同;而对圆柱形直壁容器底的压力F=ps=ρghs=ρvg=mg,可知未放小球时液体对容器底的压力关系.现在知道液体对容器底的压力相等,从而得出放入A后排开的液体重要大于放入B后排开的液体重,从而得出答案.
解答:解:∵hA=hB,pA=pB,
∴液体密度:ρA=ρB;
∵F=ps=ρghs=ρvg=mg,
∴未放入小球时,液体对A容器底的压力小于液体对B容器底的压力;
现在,将小球浸没于水中后,液体对A容器底的压力等于液体对B容器底的压力;
要求A排开液体重要比B排开液体重大,即甲球的体积大于乙球的体积.
故选D.
∴液体密度:ρA=ρB;
∵F=ps=ρghs=ρvg=mg,
∴未放入小球时,液体对A容器底的压力小于液体对B容器底的压力;
现在,将小球浸没于水中后,液体对A容器底的压力等于液体对B容器底的压力;
要求A排开液体重要比B排开液体重大,即甲球的体积大于乙球的体积.
故选D.
点评:对圆柱形直壁容器,知道液体对容器底的压力F=ps=ρghs=ρvg=mg是本题的关键.

练习册系列答案
相关题目
 (2010?锦州)如图所示为上海世博园区的一种太阳能照明灯,铭牌上标有“220V 40W LED”字样.若太阳能电池板接收太阳能的有效面积为0.5m2,该电池板每天平均能接收的太阳能为2.88×107 J/m2.若太阳照射一天,恰好可供该照明灯正常工作10h.求:
(2010?锦州)如图所示为上海世博园区的一种太阳能照明灯,铭牌上标有“220V 40W LED”字样.若太阳能电池板接收太阳能的有效面积为0.5m2,该电池板每天平均能接收的太阳能为2.88×107 J/m2.若太阳照射一天,恰好可供该照明灯正常工作10h.求: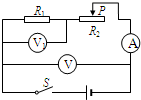 (2010?上海二模)在如图所示的电路中,电源电压保持不变.电阻R1的阻值 为20欧,滑动变阻器R2上标有“20Ω,2A”字样.闭合电键S后,当滑动变阻器的滑片P在中点位置时,电压表V1的示数为4伏.求:
(2010?上海二模)在如图所示的电路中,电源电压保持不变.电阻R1的阻值 为20欧,滑动变阻器R2上标有“20Ω,2A”字样.闭合电键S后,当滑动变阻器的滑片P在中点位置时,电压表V1的示数为4伏.求: (2010?上海二模)如图所示的装置是
(2010?上海二模)如图所示的装置是 (2010.上海)如图所示,两端开口的圆筒内嵌有一凸透镜,透镜主光轴恰好与圆筒中轴线重合.为了测出该透镜的焦距以及透镜在圆筒内的位置,小李同学做如下实验:在圆筒左侧凸透镜的主光轴上放置一点光源S,在圆筒右侧垂直凸透镜的主光轴固定一光屏,点光源S与光屏的距离为L.左右移动圆筒,当圆筒左端面距离点光源S为a时,恰好在光屏上成一个清晰的像;将圆筒向右水平移动距离b,光屏上又出现了一个清晰的像.则凸透镜和圆筒左端面的距离x为
(2010.上海)如图所示,两端开口的圆筒内嵌有一凸透镜,透镜主光轴恰好与圆筒中轴线重合.为了测出该透镜的焦距以及透镜在圆筒内的位置,小李同学做如下实验:在圆筒左侧凸透镜的主光轴上放置一点光源S,在圆筒右侧垂直凸透镜的主光轴固定一光屏,点光源S与光屏的距离为L.左右移动圆筒,当圆筒左端面距离点光源S为a时,恰好在光屏上成一个清晰的像;将圆筒向右水平移动距离b,光屏上又出现了一个清晰的像.则凸透镜和圆筒左端面的距离x为