题目内容
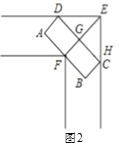
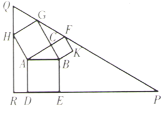
【题目】如图，
中，
，
，
，分别以
、
、
为边作正方形
、
、
，再作
，使
，点
在边
上，点
、
在边
上，点
、
在边
上，则的长为__________．
【答案】
【解析】
首先证明△ABC≌△GFC（SAS），利用全等三角形的性质可得：∠CGF=∠BAC=30°，在直角△ABC中，根据三角函数即可求得AC，进而由等边三角形的性质和正方形的性质及三角函数就可求得QR的长，在直角△QRP中运用三角函数即可得到RP、进而可求出PQ的长.
延长BA交QR于点M
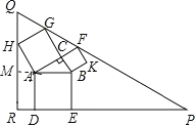
在△ABC和△GFC中
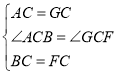
∴△ABC≌△GFC（SAS）
∴∠CGF=∠CAB=30°
∴∠HGQ=180°-∠HGC-∠CGF =180°-90°-30°=60°
∴∠HAM=180°-∠HAC-∠CAB =180°-90°-30°=60°
∵∠R=∠ADE=90°
∴QR∥AD
∴BM⊥QR
∴四边形RDAM是矩形
∴∠MHA+∠HAM=∠MHA+∠QHG=90°
∴∠QHG=60°
∴△QHG是等边三角形
∴
则
在直角△HMA中，
∵四边形RDAM是矩形
∴MR=AD=AB=4
∴
∴
故填：.
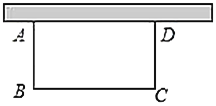
举一反三期末百分冲刺卷系列答案【题目】如图，用一段长为
的篱笆围成一个一边靠墙的矩形花圃
，墙长
．设
长为
，矩形的面积为
．
（1）写出
与
的函数关系式；当长为多少米时，所围成的花圃面积最大？最大值是多少？
（2）当花圃的面积为
时，长为多少米？
【题目】温州某企业安排65名工人生产甲、乙两种产品，每人每天生产2件甲或1件乙，甲产品每件可获利15元．根据市场需求和生产经验，乙产品每天产量不少于5件，当每天生产5件时，每件可获利120元，每增加1件，当天平均每件获利减少2元．设每天安排x人生产乙产品．
（1）根据信息填表
产品种类 | 每天工人数（人） | 每天产量（件） | 每件产品可获利润（元） |
甲 | 15 | ||
乙 |
|
|
（2）若每天生产甲产品可获得的利润比生产乙产品可获得的利润多550元，求每件乙产品可获得的利润．
（3）该企业在不增加工人的情况下，增加生产丙产品，要求每天甲、丙两种产品的产量相等．已知每人每天可生产1件丙（每人每天只能生产一件产品），丙产品每件可获利30元，求每天生产三种产品可获得的总利润W（元）的最大值及相应的x值．
