Question

已知二次函数y=-

1

2

(x-

3

2

)2+

25

8

的图象在坐标原点为O的直角坐标系中，
（1）设这个二次函数的图象与x轴的交点是A、B（B在点A右边），与y轴的交点是C，求A、B、C的坐标；
（2）求证：△OAC∽△OCB．

Answer 1

分析：（1）利用图象与x轴相交y=0，求出图象与x轴交点坐标即可，以及与y轴交点坐标即可．
（2）利用各点坐标得出AO=1，BO=4，OC=2，再利用相似三角形的判定求出即可．

解答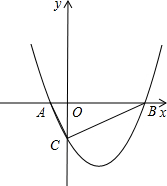：解：（1）把（x，0）代入y=-

1

2

(x-

3

2

)2+

25

8

中
得：0=-

1

2

(x-

3

2

)2+

25

8

，解得：A（-1，0），B（4，0），
把（0，y）代入解得：C（0，2），
（2）由A（-1，0），B（4，0），C（0，2）可得，
AO=1，BO=4，OC=2，
∴

AO

OC

=

OC

BO

=

1

2

．
又∵∠AOC=∠COB
∴△AOC∽△COB．

点评：此题主要考查了图象与坐标轴交点坐标求法以及相似三角形的判定，求出AO=1，BO=4，OC=2长是解题关键．