题目内容
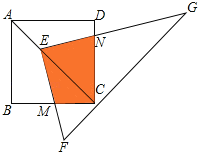
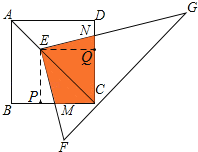
【题目】如图，点E在正方形ABCD的对角线AC上，且EC=2AE，直角三角形FEG的两直角边EF、EG分别交BC、DC于点M、N．若正方形ABCD的边长为a，则重叠部分四边形EMCN的面积为（ ）
A．
a2 B．
a2 C．
a2 D．
a2
【答案】D．
【解析】
试题分析：过E作EP⊥BC于点P，EQ⊥CD于点Q，△EPM≌△EQN，利用四边形EMCN的面积等于正方形PCQE的面积求解．
解：过E作EP⊥BC于点P，EQ⊥CD于点Q，
∵四边形ABCD是正方形，
∴∠BCD=90°，
又∵∠EPM=∠EQN=90°，
∴∠PEQ=90°，
∴∠PEM+∠MEQ=90°，
∵三角形FEG是直角三角形，
∴∠NEF=∠NEQ+∠MEQ=90°，
∴∠PEM=∠NEQ，
∵AC是∠BCD的角平分线，∠EPC=∠EQC=90°，
∴EP=EQ，四边形PCQE是正方形，
在△EPM和△EQN中，
，
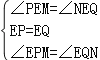∴△EPM≌△EQN（ASA）
∴S△EQN=S△EPM，
∴四边形EMCN的面积等于正方形PCQE的面积，
∵正方形ABCD的边长为a，
∴AC=
a，
∵EC=2AE，
∴EC=
a，
∴EP=PC=
a，
∴正方形PCQE的面积=a×a=
a2，
∴四边形EMCN的面积=a2，
故选：D．
练习册系列答案
相关题目
