题目内容
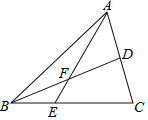
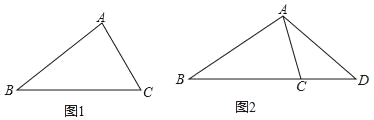
【题目】问题背景 如图1,在△ABC中,BC=4,AB=2AC.
问题初探 请写出任意一对满足条件的AB与AC的值:AB= ,AC= .
问题再探 如图2,在AC右侧作∠CAD=∠B,交BC的延长线于点D,求CD的长.
问题解决 求△ABC的面积的最大值.
【答案】(1)6、3;(2)![]() ;(3)
;(3)![]()
【解析】试题分析:(1)设AC=x,则AB=2x,根据三角形的三边关系,求出x的取值范围,然后取一个符合条件的值即可;
(2)根据两角对应相等的两三角形相似,可证明△DAC∽△DBA,然后根据相似三角形的对应边成比例,代入即可构成方程组求解;
(3)设AC=m、则AB=2m,根据锐角三角函数表示出△ABC的面积,然后由余弦定理,可求得cosC的关系式,再代入面积的关系式,配方后,根据二次函数的最值求解即可.
试题解析:问题初探,设AC=x,则AB=2x,
∵BC=4,
∴2x﹣x<4且2x+x>4,
解得: ![]() <x<4,
<x<4,
取x=3,则AC=3、AB=6,
故答案为:6、3;
问题再探,∵∠CAD=∠B,∠D=∠D,
∴△DAC∽△DBA,
则![]() =
=![]() =
=![]() ,
,
设CD=a、AD=b,
∴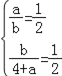 ,
,
解得:![]() ,
,
即CD=![]() ;
;
问题解决,设AC=m、则AB=2m,
根据面积公式可得S△ABC=![]() ACBCsinC=2msinC=2m
ACBCsinC=2msinC=2m![]() ,
,
由余弦定理可得cosC=![]() ,
,
∴S△ABC=2m![]()
=2m![]()
=![]()
=
=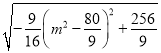
由三角形三边关系知![]() <m<4,
<m<4,
所以当m=![]() 时,S△ABC取得最大值
时,S△ABC取得最大值![]() .
.

练习册系列答案
相关题目