题目内容
【题目】下面是小丁设计的“利用直角三角形和它的斜边中点作矩形”的尺规作图过程.
已知:如图，在RtΔABC中，∠ABC=90°，0为AC的中点.
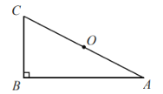
求作:四边形ABCD，使得四边形ABCD为矩形.
作法:①作射线BO，在线段BO的延长线上取点D，使得DO=BO；
②连接AD，CD，则四边形ABCD为矩形.
根据小丁设计的尺规作图过程.
(1)使用直尺和圆规，在图中补全图形(保留作图痕迹)；
(2)完成下面的证明.
证明:∴点O为AC的中点，
∴AO=CO.
又∵DO=BO，
∵四边形ABCD为平行四边形(__________)(填推理的依据).
∵∠ABC=90°，
∴
ABCD为矩形(_________)(填推理的依据).
【答案】(1)作图如图所示，见解析(2)对角线互相平分的四边形是平行四边形， 有一个角是直角的平行四边形是矩形.
【解析】
（1）根据要求画出图形即可．
（2）根据有一个角是直角的平行四边形是矩形即可证明．
（1）如图，矩形ABCD即为所求．
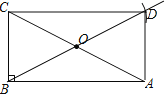
（2）理由：∵点O为AC的中点，
∴AO=CO
又∵DO=BO，
∴四边形ABCD为平行四边形（对角线互相平分的四边形是平行四边形）
∵∠ABC=90°，
∴ABCD为矩形（有一个角是直角的平行四边形是矩形）．
故答案为：对角线互相平分的四边形是平行四边形，有一个角是直角的平行四边形是矩形.
练习册系列答案
相关题目
