题目内容
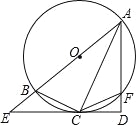
【题目】如图,已知AB为⊙O的直径,F为⊙O上一点,AC平分∠BAF且交⊙O于点C,过点C作CD⊥AF于点D,延长AB、DC交于点E,连接BC、CF.
(1)求证:CD是⊙O的切线;
(2)若AD=6,DE=8,求BE的长;
(3)求证:AF+2DF=AB.
【答案】(1)证明详见解析;(2) ![]() ;(3)证明详见解析.
;(3)证明详见解析.
【解析】
试题分析:(1)连接OC,由AB为⊙O的直径,得到∠ACB=90°,求得∠ACB=∠D,根据角平分线的性质得到∠BAC=∠CAD,通过相似三角形得到∠ABC=∠ACD,等量代换得到∠OCB=∠ACD,求出∠OCD=90°,即可得到结论;
(2)根据勾股定理得到AE=![]() =10,根据相似三角形的性质得到
=10,根据相似三角形的性质得到![]() ,代入数据得到r=
,代入数据得到r=![]() ,于是得到结论;
,于是得到结论;
(3)过C作 CG⊥AE于G,根据全等三角形的性质得到AG=AD,CG=CD,推出Rt△BCG≌Rt△FCD,由全等三角形的性质得到BG=FD,等量代换即可得到结论.
试题解析:(1)连接OC,
∵AB为⊙O的直径,
∴∠ACB=90°,
∵CD⊥AF,
∴∠D=90°,
∴∠ACB=∠D,
∵AC平分∠BAF,
∴∠BAC=∠CAD,
∴△ABC∽△ACD,
∴∠ABC=∠ACD,
∵OB=OC,
∴∠OBC=∠OCB,
∴∠OCB=∠ACD,
∵∠OCB+∠ACO=∠ACO+∠ACD=90°,
∴∠OCD=90°,
∴CD是⊙O的切线;
(2)∵AD=6,DE=8,
∴AE=![]() =10,
=10,
∵OC∥AD,
∴∠OCE=∠ADE,
∴△OCE∽△ADE,
∴![]() ,即
,即![]() ,
,
∴r=![]() ,
,
∴BE=10﹣![]() =
=![]() ;
;
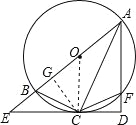
(3)过C作 CG⊥AE于G,
在△ACG与△ACD中,
∠GAC=∠DAC,∠CGA=∠CDA,AC=AC,
∴△ACG≌△ACD,
∴AG=AD,CG=CD,
∵BC=CF,
在Rt△BCG与Rt△FCD中,
CG=CD,BC=CF,
∴Rt△BCG≌Rt△FCD,
∴BG=FD,
∴AF+2DF=AD+DF=AG+GB=AB,
即AF+2DF=AB.

 阅读快车系列答案
阅读快车系列答案