Question

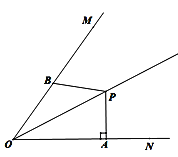
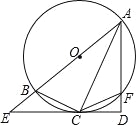
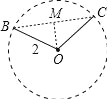
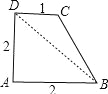
【题目】连接一个几何图形上任意两点间的线段中，最长的线段称为这个几何图形的直径，根据此定义，图（扇形、菱形、直角梯形、红十字图标）中“直径”最小的是（ ）.

A． B． C． D．

Answer 1

【答案】C．

【解析】

试题分析：先找出每个图形的“直径”，再根据所学的定理求出其长度，最后进行比较即可．A. 连接BC，则BC为这个几何图形的直径，过O作OM⊥BC于M，∵OB=OC，∴∠BOM=∠BOC=60°，∴∠OBM=30°，∵OB=2，OM⊥BC，∴OM=OB=1，由勾股定理得：BM=，∴由垂径定理得：BC=；B. 连接AC、BD，则BD为这个图形的直径，∵四边形ABCD是菱形，∴AC⊥BD，BD平分∠ABC，∵∠ABC=60°，∴∠ABO=30°，∴AO=AB=1，由勾股定理得：BO=，∴BD=2BO=；C. 连接BD，则BD为这个图形的直径，由勾股定理得：BD==；D. 连接BD，则BD为这个图形的直径，由勾股定理得：BD==，∵＞＞，∴选项A、B、D错误，选项C正确；

故选：C．