题目内容
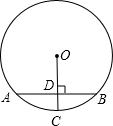（2012•汉沽区一模）如图，AB是⊙O的弦，⊙O的半径为5，OC⊥AB于D，交⊙O于点C，且CD=1，则弦AB的长为（ ）分析：连接OA，根据垂径定理求出AB=2AD，根据勾股定理得出OA2=AD2+OD2，推出52=AD2+（5-1）2，求出AD即可．
解答：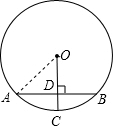
解：连接AO，
∵OC⊥AB，OC是半径，
∴AB=2AD=2BD，
在Rt△OAD中，由勾股定理得：OA2=AD2+OD2，
52=AD2+（5-1）2，
AD=3，
∴AB=6，
故选A．
解：连接AO，∵OC⊥AB，OC是半径，
∴AB=2AD=2BD，
在Rt△OAD中，由勾股定理得：OA2=AD2+OD2，
52=AD2+（5-1）2，
AD=3，
∴AB=6，
故选A．
点评：本题考查了垂径定理和勾股定理的应用，关键是构造直角三角形，用了方程思想．
练习册系列答案
海淀黄冈名师导航系列答案
普通高中同步练习册系列答案
相关题目
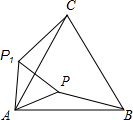（2012•汉沽区一模）△ABC是等边三角形，点P在△ABC内，PA=2，将△PAB绕点A逆时针旋转得到△P1AC，则P1P的长等于（ ）