题目内容
如图,已知O是线段AB上一点,以OB为半径作圆O交AB于点C,以线段AO为直径作弧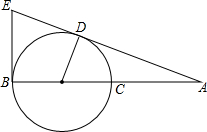 OD交圆O于点D,过点B作AB的垂线交AD的延长线于点E,若线段AO、OD的长是一元二次方程x2-3x+2=0的两根.
OD交圆O于点D,过点B作AB的垂线交AD的延长线于点E,若线段AO、OD的长是一元二次方程x2-3x+2=0的两根.
(1)求证:AE是⊙O的切线;
(2)求线段EB的长.
证明:(1)∵以线段AO为直径作弧OD交圆O于点D,
∴∠ODA=90°,即AE⊥OD.
∴AE是⊙O的切线;
(2)解方程:x1=1,x2=2,
∴OA=2,OD=1.
AD= .所以AB=3.
.所以AB=3.
设EB=x,
则EB=ED=x.
x2+9=(x+ )2
)2
x= ,即EB=
,即EB= .
.
分析:(1)欲证AE是切线,只需证AE⊥OD.根据直径所对的圆周角是直角易证;
(2)根据切线长定理得BE=ED;根据勾股定理易求AD的长;设BE=x.在Rt△ABE中,根据勾股定理得方程求解.
点评:①掌握切线的判定方法:经过半径的外端且垂直于该半径的直线是圆的切线.
②综合运用切线长定理和勾股定理解题,是圆中解直角三角形常用的方法.
∴∠ODA=90°,即AE⊥OD.
∴AE是⊙O的切线;
(2)解方程:x1=1,x2=2,
∴OA=2,OD=1.
AD=
 .所以AB=3.
.所以AB=3.设EB=x,
则EB=ED=x.
x2+9=(x+
 )2
)2x=
 ,即EB=
,即EB= .
. 分析:(1)欲证AE是切线,只需证AE⊥OD.根据直径所对的圆周角是直角易证;
(2)根据切线长定理得BE=ED;根据勾股定理易求AD的长;设BE=x.在Rt△ABE中,根据勾股定理得方程求解.
点评:①掌握切线的判定方法:经过半径的外端且垂直于该半径的直线是圆的切线.
②综合运用切线长定理和勾股定理解题,是圆中解直角三角形常用的方法.

练习册系列答案
相关题目
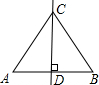 如图,已知CD是线段AB的垂直平分线,垂足为D,E是CD上一点.若∠A=60°,则下列结论中错误的是( )
如图,已知CD是线段AB的垂直平分线,垂足为D,E是CD上一点.若∠A=60°,则下列结论中错误的是( )| A、AE=BE | B、AD=BD | C、AB=AC | D、ED=AD |
如图,已知C是线段AB的中点,则CD等于( )


| A、AD-BD | ||
B、
| ||
C、
| ||
D、AD-
|
 如图,已知B是线段AE上一点,ABCD和BEFG都是正方形,连接AG、CE.
如图,已知B是线段AE上一点,ABCD和BEFG都是正方形,连接AG、CE. (2012•宿迁)如图,已知P是线段AB的黄金分割点,且PA>PB,若S1表示PA为一边的正方形的面积,S2表示长是AB,宽是PB的矩形的面积,则S1
(2012•宿迁)如图,已知P是线段AB的黄金分割点,且PA>PB,若S1表示PA为一边的正方形的面积,S2表示长是AB,宽是PB的矩形的面积,则S1