题目内容
下列叙述中正确的是( )
分析:分别根据勾股定理、勾股定理的逆定理及三角形内角和定理对各选项进行逐一分析即可.
解答:解:A、直角三角形中,两条直角边的平方和等于第三边的平方,故本选项错误;
B、∵三角形三个内角度数之比为3:4:5,
∴设三角形的三个内角分别为3x,4x,5x,则3x+4x+5x=180°,解得x=15°,∴5x=75°,
∴该三角形不是直角三角形,故本选项错误;
C、在△ABC中,∠A、∠B、∠C的对边分别为a,b,c,若c2-a2=b2,则∠C=90°,故本选项错误;
D、∵a2+b2+c2+50=6a+8b+10c,
∴a2-6a+9+b2-8b+16+c2-10c+25=0,即(a-3)2+(b-4)2+(c-5)2=0,
∴a=3,b=4,c=5,
∵32+42=52,
∴△ABC是直角三角形,故本选项正确.
故选D.
B、∵三角形三个内角度数之比为3:4:5,
∴设三角形的三个内角分别为3x,4x,5x,则3x+4x+5x=180°,解得x=15°,∴5x=75°,
∴该三角形不是直角三角形,故本选项错误;
C、在△ABC中,∠A、∠B、∠C的对边分别为a,b,c,若c2-a2=b2,则∠C=90°,故本选项错误;
D、∵a2+b2+c2+50=6a+8b+10c,
∴a2-6a+9+b2-8b+16+c2-10c+25=0,即(a-3)2+(b-4)2+(c-5)2=0,
∴a=3,b=4,c=5,
∵32+42=52,
∴△ABC是直角三角形,故本选项正确.
故选D.
点评:本题考查的是勾股定理的逆定理即三角形内角和定理,熟知如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形是解答此题的关键.

练习册系列答案
相关题目
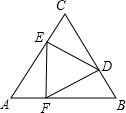 用三个全等的直角三角形△AEF、△BDF和△CDE拼成如图所示的大的正三角形,已知大的正三角形的边长是3,则下列叙述中正确的是
用三个全等的直角三角形△AEF、△BDF和△CDE拼成如图所示的大的正三角形,已知大的正三角形的边长是3,则下列叙述中正确的是 图中的点均为大小相同的小正方形的顶点,对于所画的两个四边形,下列叙述中正确的是( )
图中的点均为大小相同的小正方形的顶点,对于所画的两个四边形,下列叙述中正确的是( ) 如图所示,两个四边形的顶点都在格点上,记四边形ABCD的面积为SⅠ,周长为CⅠ;四边形A′B′C′D′的面积为SⅡ,周长为CⅡ,下列叙述中正确的是( )
如图所示,两个四边形的顶点都在格点上,记四边形ABCD的面积为SⅠ,周长为CⅠ;四边形A′B′C′D′的面积为SⅡ,周长为CⅡ,下列叙述中正确的是( )