题目内容
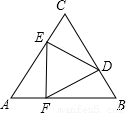
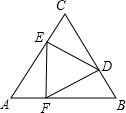用三个全等的直角三角形△AEF、△BDF和△CDE拼成如图所示的大的正三角形，已知大的正三角形的边长是3，则下列叙述中正确的是①∠A=60°；②△DEF是等边三角形；③△DEF的边长为2；④△DEF的面积为
| 3 |
| 4 |
| 3 |
分析：由题可知△AEF≌△BDF≌△CDE，从而推EFD是全等三角形，因为已知∠A=60°，∠EFD=60°，∠EFA=90°，所以∠DFB=30°，因此DB=1，BF=2，可推出DF=
，故△DEF的边长为
．而△DEF的高为
，所以面积为
．
| 3 |
| 3 |
| 3 |
| 2 |
3
| ||
| 4 |
解答：解：∵△ACB为等边三角形
∴∠A=60°
∴△AEF≌△BDF≌△CDE
∴ED=EF=BF
∴△EFD是全等三角形
已知∠A=60°，∠EFD=60°，∠EFA=90°
∴∠DFB=30°
∴DB=1，BF=2
∴DF=
，
∴△DEF的边长为
．
∵△DEF的高为
，
∴面积为
．
∴∠A=60°
∴△AEF≌△BDF≌△CDE
∴ED=EF=BF
∴△EFD是全等三角形
已知∠A=60°，∠EFD=60°，∠EFA=90°
∴∠DFB=30°
∴DB=1，BF=2
∴DF=
| 3 |
∴△DEF的边长为
| 3 |
∵△DEF的高为
| 3 |
| 2 |
∴面积为
3
| ||
| 4 |
点评：本题考查了等边三角形的性质以及全等三角形的判定定理的有关知识，难度中等．
练习册系列答案
相关题目
用三个全等的直角三角形△AEF、△BDF和△CDE拼成如图所示的大的正三角形，已知大的正三角形的边长是3，则下列叙述中正确的是________．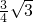
．
．
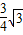