题目内容
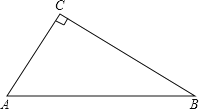
【题目】如图,在等腰△ABC中,AB=AC=4,BC=6点D在底边BC上,且∠DAC=∠ACD,将△ACD沿着AD所在直线翻折,使得点C落到点E处,联结BE,那么BE的长为______.
【答案】1
【解析】
只要证明△ABD∽△MBE,得![]() ,只要求出BM、BD即可解决问题.
,只要求出BM、BD即可解决问题.
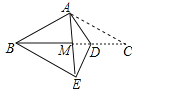
∵AB=AC,
∴∠ABC=∠C,
∵∠DAC=∠ACD,
∴∠DAC=∠ABC,
∵∠C=∠C,
∴△CAD∽△CBA,
∴![]()
∴![]() ,
,
∴CD=![]() ,BD=BC-CD=6-
,BD=BC-CD=6-![]() =
=![]() ,
,
∵∠DAM=∠DAC=∠DBA,∠ADM=∠ADB,
∴△ADM∽△BDA,
∴![]() ,即
,即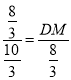 ,
,
∴DM=![]() ,MB=BD-DM=
,MB=BD-DM=![]() -
-![]() =
=![]() ,
,
∵∠ABM=∠C=∠MED,
∴A、B、E、D四点共圆,
∴∠ADB=∠BEM,∠EBM=∠EAD=∠ABD,
∴△ABD∽△MBE,
∴![]() ,
,
∴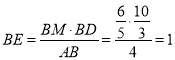 .
.

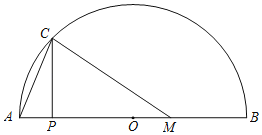
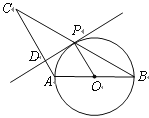
【题目】如图,在半圆弧AB中,直径AB=6cm,点M是AB上一点,MB=2cm,P为AB上一动点,PC⊥AB交AB于点C,连接AC和CM,设A、P两点间的距离为xcm,A、C两点间的距离为y1cm,C、M两点间的距离为y2cm.
小东根据学习函数的经验,分别对函数y1、y2随自变量x的变化而变化的规律进行了探究:
下面是小东的探究过程,请补充完整:
(1)按照下表中自变量x的值进行取点、画图、测量,分别得到了y1,y2与x的几组对应值;
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
y1/cm | 0 | 2.45 | 3.46 | 4.90 | 5.48 | 6 | |
y2/cm | 4 | 3.74 | 3.46 | 3.16 | 2.83 | 2.45 | 2 |
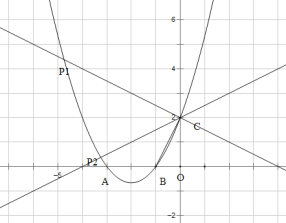
(2)在同一平面直角坐标系xOy中,描出补全后的表中各组数值所对应的点(x,y1),(x,y2),并画出函数y1,y2的图象;

(3)结合函数图象,解决问题:
①当AC>CM时,线段AP的取值范围是 ;
②当△AMC是等腰三角形时,线段AP的长约为 .