题目内容
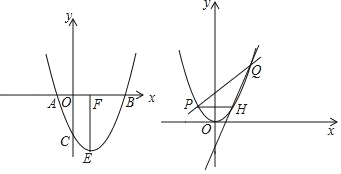
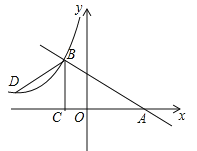
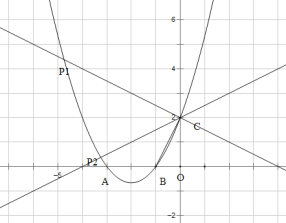
【题目】已知:在平面直角坐标系xOy中,对称轴为直线x = -2的抛物线经过点C(0,2),与x轴交于A(-3,0)、B两点(点A在点B的左侧).
(1)求这条抛物线的表达式.
(2)连接BC,求∠BCO的余切值.
(3)如果过点C的直线,交x轴于点E,交抛物线于点P,且∠CEO =∠BCO,求点P的坐标.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)点P坐标是(
;(3)点P坐标是(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).
【解析】
(1)首先设抛物线的解析式,然后根据对称轴和所经过的点,列出方程,即可得出解析式;
(2)首先求出B坐标,即可得出![]() ,
,![]() ,进而得出∠BCO的余切值;
,进而得出∠BCO的余切值;
(3)首先根据![]() 的余切值列出等式,得出点E的坐标,然后根据点C的坐标得出直线解析式,最后联立直线和抛物线的解析式即可得出点P坐标.
的余切值列出等式,得出点E的坐标,然后根据点C的坐标得出直线解析式,最后联立直线和抛物线的解析式即可得出点P坐标.
(1)设抛物线的表达式为![]() .
.
由题意得: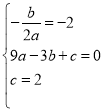
解得:![]() ,
,![]() .
.
∴这条抛物线的表达式为![]() .
.
(2)令y = 0,那么![]() ,
,
解得![]() ,
,![]() .
.
∵点A的坐标是(![]() 3,0)
3,0)
∴点B的坐标是(![]() 1,0).
1,0).
∵C(0,2)
∴![]() ,
,![]() .
.
在Rt△ OBC中,∠BOC=90,
∴![]() .
.
(3)设点E的坐标是(x,0),得OE=![]() .
.
∵![]() ,
,
∴![]() .
.
在Rt△EOC中,∴![]() .
.
∴![]() =4,∴点E坐标是(4,0)或 (
=4,∴点E坐标是(4,0)或 (![]() 4,0).
4,0).
∵点C坐标是(0,2),
∴![]() .
.
∴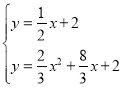 ,或
,或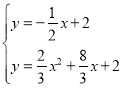
解得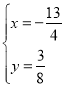 和
和![]() (舍去),或
(舍去),或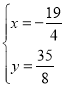 和
和![]() (舍去);
(舍去);
∴点P坐标是(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).

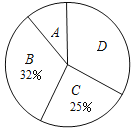
【题目】在“书香校园”活动中,某校为了解学生家庭藏书情况,随机抽取本校部分学生进行调查,并绘制成部分统计图表如下:
类别 | 家庭藏书m本 | 学生人数 |
A | 0≤m≤25 | 20 |
B | 26≤m≤50 | a |
C | 51≤m≤75 | 50 |
D | m≥76 | 66 |
根据以上信息,解答下列问题:
(1)该调查的样本容量为 ,a= ;
(2)随机抽取一位学生进行调查,刚好抽到A类学生的概率是 ;
(3)若该校有2000名学生,请估计全校学生中家庭藏书不少于76本的人数.