题目内容
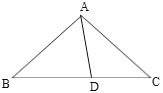
【题目】如图,在Rt△ABC中,∠ACB=90°.
(1)利用尺规作图,在BC边上求作一点P,使得点P到边AB的距离等于PC的长;(要求:尺规作图,不写作法,保留作图痕迹,并把作图痕迹用黑色签字笔描黑)
(2)在(1)的条件下,以点P为圆心,PC长为半径的⊙P中,⊙P与边BC相交于点D,若AC=6,PC=3,求BD的长.
【答案】(1)如图所示,见解析;(2)BD的长为2.
【解析】
(1)根据题意可知要作∠A的平分线,按尺规作图的要求作角平分线即可;
(2)由切线长定理得出AC=AE,设BD=x,BE=y,则BC=6+x,BP=3+x,通过△PEB∽△ACB可得出![]() ,从而建立一个关于x,y的方程,解方程即可得到BD的长度.
,从而建立一个关于x,y的方程,解方程即可得到BD的长度.
(1)如图所示:
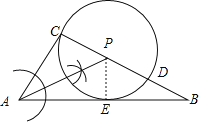
作∠A的平分线交BC于点P,
点P即为所求作的点.
(2)作PE⊥AB于点E,则PE=PC=3,
∴AB与圆相切,
∵∠ACB=90°,
∴AC与圆相切,
∴AC=AE,
设BD=x,BE=y,
则BC=6+x,BP=3+x,
∵∠B=∠B,∠PEB=∠ACB,
∴△PEB∽△ACB
∴![]()
∴![]()
解得x=2,
答:BD的长为2.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目