题目内容
【题目】在直角坐标系![]() 中,
中,![]() 、
、![]() ,将
,将![]() 经过旋转、平移变化后得到如图1所示的
经过旋转、平移变化后得到如图1所示的![]() .
.
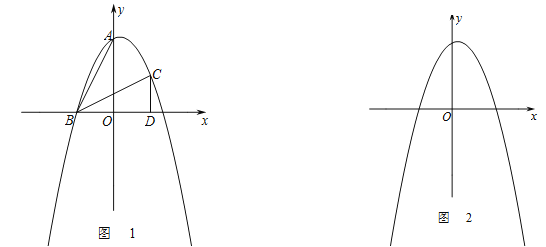
(1)求经过![]() 、
、![]() 、
、![]() 三点的抛物线的解析式;
三点的抛物线的解析式;
(2)连结![]() ,点
,点![]() 是位于线段
是位于线段![]() 上方的抛物线上一动点,若直线
上方的抛物线上一动点,若直线![]() 将
将![]() 的面积分成
的面积分成![]() 两部分,求此时点
两部分,求此时点![]() 的坐标;
的坐标;
(3)现将![]() 、
、![]() 分别向下、向左以
分别向下、向左以![]() 的速度同时平移,求出在此运动过程中
的速度同时平移,求出在此运动过程中![]() 与
与![]() 重叠部分面积的最大值.
重叠部分面积的最大值.
【答案】(1)![]() ;(2)
;(2)![]() ,
,![]() ;(3)
;(3)![]() .
.
【解析】
试题分析:(1)先根据平移性质写出C点坐标,设经过![]() 、
、![]() 、
、![]() 三点的抛物线解析式为
三点的抛物线解析式为![]() ,然后将A,B,C三点坐标代入解析式,求出a,b,c即可确定此抛物线解析式;(2)分两种情况计算,设直线
,然后将A,B,C三点坐标代入解析式,求出a,b,c即可确定此抛物线解析式;(2)分两种情况计算,设直线![]() 与
与![]() 交于点
交于点![]() . ∵直线
. ∵直线![]() 将
将![]() 的面积分成
的面积分成![]() 两部分,∴
两部分,∴![]() 或
或![]() ,过
,过![]() 作
作![]() 于点
于点![]() ,则
,则![]() ∥
∥![]() .∴
.∴![]() ∽
∽![]() ,∴
,∴![]() .∴当
.∴当![]() 时,
时,![]() ,能求出EF,BF,的长度,再求出OF的长度,于是E点坐标确定,直线EC的解析式也就知道了,因为P点在直线EC上,又在抛物线上,列两解析式相等,即可求出P点横坐标,代入两个中任何一个解析式就可求出P点纵坐标.当
,能求出EF,BF,的长度,再求出OF的长度,于是E点坐标确定,直线EC的解析式也就知道了,因为P点在直线EC上,又在抛物线上,列两解析式相等,即可求出P点横坐标,代入两个中任何一个解析式就可求出P点纵坐标.当![]() 时,同样有
时,同样有![]() ,于是有
,于是有![]() ,同样求出EF,BF,的长度,再求出OF的长度,确定E点坐标及直线EC的解析式,列两解析式相等,进而求出P点坐标;(3)设
,同样求出EF,BF,的长度,再求出OF的长度,确定E点坐标及直线EC的解析式,列两解析式相等,进而求出P点坐标;(3)设![]() 向下平移的距离为
向下平移的距离为![]() ,则△CBD向左平移的距离为2t,
,则△CBD向左平移的距离为2t,![]() 与
与![]() 重叠部分的面积为
重叠部分的面积为![]() .当C点向左平移到A1B1边上时,两三角形重叠部分由四边形变为直角三角形,算出t=
.当C点向左平移到A1B1边上时,两三角形重叠部分由四边形变为直角三角形,算出t=![]() ,即当
,即当![]() 时,
时,![]() 与
与![]() 重叠部分为四边形.设
重叠部分为四边形.设![]() 与
与![]() 轴交于点
轴交于点![]() ,
,![]() 与
与![]() 轴交于点
轴交于点![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,连结
,连结![]() .由已知求出
.由已知求出![]() 的解析式,
的解析式,![]() 的解析式,
的解析式,![]() 与
与![]() 轴交点坐标,
轴交点坐标,![]() 与
与![]() 轴交点坐标,两个解析式联立求出Q点坐标,建立重叠部分S与t的二次函数并算出最大值.平移过程中当D点与
轴交点坐标,两个解析式联立求出Q点坐标,建立重叠部分S与t的二次函数并算出最大值.平移过程中当D点与![]() 交于x轴同一点时,这时重叠部分为0,算出t=
交于x轴同一点时,这时重叠部分为0,算出t=![]() ,即当
,即当![]() 时,
时,![]() 与
与![]() 重叠部分为直角三角形.设
重叠部分为直角三角形.设![]() 与
与![]() 轴交于点
轴交于点![]() ,
, ![]() 与
与![]() 交于点
交于点![]() .则
.则![]() ,利用三角形相似或平移的距离表示出重叠部分三角形的底和高,建立S与t的二次函数,算出最大值,两种情况进行比较,得出结论.
,利用三角形相似或平移的距离表示出重叠部分三角形的底和高,建立S与t的二次函数,算出最大值,两种情况进行比较,得出结论.
试题解析:(1)由题意可知![]() 、
、![]() ,将
,将![]() 经过旋转、平移变化得到如图所示的
经过旋转、平移变化得到如图所示的![]() ,
,
∴![]() .∴
.∴![]() .设经过
.设经过![]() 、
、![]() 、
、![]() 三点的抛物线解析式为
三点的抛物线解析式为![]() ,则有
,则有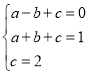 ,解得:
,解得:![]() . ∴经过
. ∴经过![]() 、
、![]() 、
、![]() 三点的抛物线的解析式为
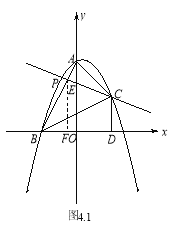
三点的抛物线的解析式为![]() ;(2)如图4.1所示,设直线
;(2)如图4.1所示,设直线![]() 与
与![]() 交于点
交于点![]() . ∵直线
. ∵直线![]() 将
将![]() 的面积分成
的面积分成![]() 两部分,∴
两部分,∴![]() 或
或![]() ,过
,过![]() 作
作![]() 于点
于点![]() ,则
,则![]() ∥
∥![]() .∴
.∴![]() ∽
∽![]() ,∴
,∴![]() .∴当
.∴当![]() 时,有
时,有![]() ,∴
,∴![]() ,∴
,∴![]() .设直线
.设直线![]() 解析式为
解析式为![]() ,将E,C两点坐标代入,则可求得其解析式为
,将E,C两点坐标代入,则可求得其解析式为![]() ,∴
,∴![]() ,解得
,解得![]() (舍去),∴
(舍去),∴![]() ;当
;当![]() 时,同样有
时,同样有![]() ∽
∽![]() ,∴
,∴![]() .即
.即![]() ,解得EF=
,解得EF=![]() ,BF=
,BF=![]() ,OF=
,OF=![]() ,所以E(-
,所以E(-![]() ,
,![]() ),设直线
),设直线![]() 解析式为
解析式为![]() ,将E,C两点坐标代入,则可求得其解析式为
,将E,C两点坐标代入,则可求得其解析式为![]() ,于是有
,于是有![]() ,整理得:
,整理得:![]() ,解得
,解得![]() (舍去),将
(舍去),将![]() 代入直线EC解析式求出y=
代入直线EC解析式求出y=![]() ,所以
,所以![]() .综上所述点P的坐标为
.综上所述点P的坐标为![]() ,
,![]() ;
;
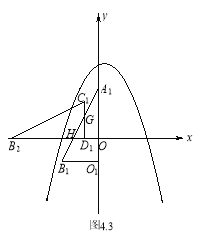
(3)设![]() 向下平移的距离为
向下平移的距离为![]() ,则△CBD向左平移的距离为2t,
,则△CBD向左平移的距离为2t,![]() 与
与![]() 重叠部分的面积为
重叠部分的面积为![]() .可由已知求出
.可由已知求出![]() 的解析式为
的解析式为![]() ,
,![]() 与
与![]() 轴交点坐标为
轴交点坐标为![]() .
. ![]() 的解析式为
的解析式为![]() ,
,![]() 与
与![]() 轴交点坐标为
轴交点坐标为![]() . ①当C点向左平移到A1B1边上时,两三角形重叠部分由四边形变为直角三角形,由平行相似可得关系式:
. ①当C点向左平移到A1B1边上时,两三角形重叠部分由四边形变为直角三角形,由平行相似可得关系式: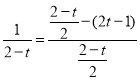 ,解得t=
,解得t=![]() ,即当
,即当![]() 时,
时,![]() 与
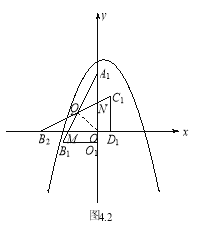
与![]() 重叠部分为四边形.如图4.2所示,设
重叠部分为四边形.如图4.2所示,设![]() 与
与![]() 轴交于点
轴交于点![]() ,
,![]() 与
与![]() 轴交于点
轴交于点![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,连结
,连结![]() .由
.由 ,得
,得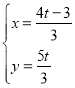 ,解得
,解得![]() .∴
.∴![]()
![]() .即当t=
.即当t=![]() 时
时![]() 的最大值为
的最大值为![]() .②平移过程中当D点与
.②平移过程中当D点与![]() 交于x轴同一点时,这时重叠部分面积为0,由DO∥
交于x轴同一点时,这时重叠部分面积为0,由DO∥![]() 可得关系式:
可得关系式:![]() ,解得t=
,解得t=![]() 如图
如图![]() 所示,即当
所示,即当![]() 时,
时,![]() 与
与![]() 重叠部分为直角三角形. 设
重叠部分为直角三角形. 设![]() 与
与![]() 轴交于点
轴交于点![]() ,
, ![]() 与
与![]() 交于点
交于点![]() .G点横坐标为1-2t,设G点纵坐标为x,则
.G点横坐标为1-2t,设G点纵坐标为x,则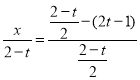 ,解得x=4-5t,于是G点坐标为
,解得x=4-5t,于是G点坐标为![]() ,则
,则![]() ,
,![]() .∴
.∴![]() .即当t=
.即当t=![]() 时,S最大值是
时,S最大值是![]() ,∴当
,∴当![]() 时,
时,![]() 的最大值为
的最大值为![]() .因为
.因为![]() <
<![]() ,所以在此运动过程中
,所以在此运动过程中![]() 与
与![]() 重叠部分面积的最大值为
重叠部分面积的最大值为![]() .
.

 阅读快车系列答案
阅读快车系列答案