题目内容
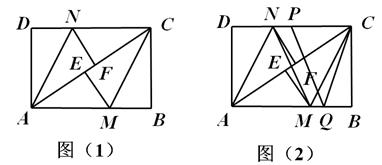
已知:如图,在菱形ABCD中,F为边BC的中点,DF与对角线AC交于点M,过M作ME⊥CD于点E,∠1=∠2.
(1)若CE=1,求BC的长;
(2)求证:AM=DF+ME.
(1)若CE=1,求BC的长;
(2)求证:AM=DF+ME.

(1)解:∵四边形ABCD是菱形,
∴AB∥CD,
∴∠1=∠ACD,
∵∠1=∠2,
∴∠ACD=∠2,
∴MC=MD,
∵ME⊥CD,
∴CD=2CE,
∵CE=1,
∴CD=2,
∴BC=CD=2;
(2)证明:如图,∵F为边BC的中点,
∴BF=CF= BC,
BC,
∴CF=CE,
在菱形ABCD中,AC平分∠BCD,
∴∠ACB=∠ACD,
在△CEM和△CFM中,
∵ ,
,
∴△CEM≌△CFM(SAS),
∴ME=MF,
延长AB交DF于点G,
∵AB∥CD,
∴∠G=∠2,
∵∠1=∠2,
∴∠1=∠G,
∴AM=MG,
在△CDF和△BGF中,
∵ ,
,
∴△CDF≌△BGF(AAS),
∴GF=DF,
由图形可知,GM=GF+MF,
∴AM=DF+ME.

∴AB∥CD,
∴∠1=∠ACD,
∵∠1=∠2,
∴∠ACD=∠2,
∴MC=MD,
∵ME⊥CD,
∴CD=2CE,
∵CE=1,
∴CD=2,
∴BC=CD=2;
(2)证明:如图,∵F为边BC的中点,
∴BF=CF=
 BC,
BC,∴CF=CE,
在菱形ABCD中,AC平分∠BCD,
∴∠ACB=∠ACD,
在△CEM和△CFM中,
∵
 ,
,∴△CEM≌△CFM(SAS),
∴ME=MF,
延长AB交DF于点G,
∵AB∥CD,
∴∠G=∠2,
∵∠1=∠2,
∴∠1=∠G,
∴AM=MG,
在△CDF和△BGF中,
∵
 ,
,∴△CDF≌△BGF(AAS),
∴GF=DF,
由图形可知,GM=GF+MF,
∴AM=DF+ME.

(1)根据菱形的对边平行可得AB∥D,再根据两直线平行,内错角相等可得∠1=∠ACD,所以∠ACD=∠2,根据等角对等边的性质可得CM=DM,再根据等腰三角形三线合一的性质可得CE=DE,然后求出CD的长度,即为菱形的边长BC的长度;
(2)先利用“边角边”证明△CEM和△CFM全等,根据全等三角形对应边相等可得ME=MF,延长AB交DF于点G,然后证明∠1=∠G,根据等角对等边的性质可得AM=GM,再利用“角角边”证明△CDF和△BGF全等,根据全等三角形对应边相等可得GF=DF,最后结合图形GM=GF+MF即可得证.
(2)先利用“边角边”证明△CEM和△CFM全等,根据全等三角形对应边相等可得ME=MF,延长AB交DF于点G,然后证明∠1=∠G,根据等角对等边的性质可得AM=GM,再利用“角角边”证明△CDF和△BGF全等,根据全等三角形对应边相等可得GF=DF,最后结合图形GM=GF+MF即可得证.

练习册系列答案
相关题目
 的边长为
的边长为 .
. 的顶点
的顶点 在边
在边 上,顶点
上,顶点 在边
在边 上.在正三角形
上.在正三角形 为位似中心,作正方形
为位似中心,作正方形 ,且使正方形
,且使正方形 和正方形
和正方形 ,使得
,使得 在边
在边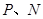 分别在边
分别在边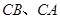 上,求这两个正方形面积和的最大值及最小值,并说明理由.
上,求这两个正方形面积和的最大值及最小值,并说明理由. 是矩形ABCD的“减半”矩形.
是矩形ABCD的“减半”矩形.

 的正方形存在“减半”正方形吗?如果存在,求出“减半”正方形的边长;如果不存在,说明理由.
的正方形存在“减半”正方形吗?如果存在,求出“减半”正方形的边长;如果不存在,说明理由.  ,AD的垂直平分线交对角线BD于点P,垂足为E,连接CP,则
,AD的垂直平分线交对角线BD于点P,垂足为E,连接CP,则 ________度.
________度.


