题目内容
如图1,将由5个边长为1的小正方形组成的十字形纸板沿虚线剪拼成一个大正方形,需剪4
刀。

(1) 思考发现:大正方形的面积等于5个小正方形的面积和,大正方形的边长等于_______。
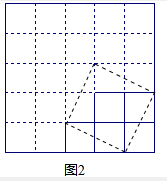
(2) 实践操作:如图2,将网格中5个边长为1的小正方形组成的图形纸板剪拼成一个大正方形,要求剪
两刀,画出剪拼的痕迹。
(3) 智力开发:将网格中的5个边长为1的正方形组成的十字形纸板,要求只剪2刀也拼成一个大正方形。
在图中用虚线画出剪拼的痕迹。
刀。

(1) 思考发现:大正方形的面积等于5个小正方形的面积和,大正方形的边长等于_______。
(2) 实践操作:如图2,将网格中5个边长为1的小正方形组成的图形纸板剪拼成一个大正方形,要求剪
两刀,画出剪拼的痕迹。
(3) 智力开发:将网格中的5个边长为1的正方形组成的十字形纸板,要求只剪2刀也拼成一个大正方形。
在图中用虚线画出剪拼的痕迹。
(1)∵小正方形的边长为1,
∴小正方形的面积为1,
∴大正方形的面积为5×1=5,
∴大正方形的边长为 ;
;
(2)如图2所示:
(3)如图3所示:

∴小正方形的面积为1,
∴大正方形的面积为5×1=5,
∴大正方形的边长为
 ;
;(2)如图2所示:

(3)如图3所示:

(1)易得5个小正方形的面积,那么就得到了大正方形的面积,求得面积的算术平方根即可为大正方形的边长;
(2)根据5个小正方形的面积的和等于拼成的正方形的面积,根据勾股定理确定截线的长度,即可确定分法;
(3)设十字形的12个顶点从上至下依次为:ABCDEFGHIJKL再设EF的中点为M,设KL的中点为N,则第一刀:MN,第二刀:CI,之后把切出的四块拼一拼,就能得到一个正方形.
(2)根据5个小正方形的面积的和等于拼成的正方形的面积,根据勾股定理确定截线的长度,即可确定分法;
(3)设十字形的12个顶点从上至下依次为:ABCDEFGHIJKL再设EF的中点为M,设KL的中点为N,则第一刀:MN,第二刀:CI,之后把切出的四块拼一拼,就能得到一个正方形.

练习册系列答案
相关题目






 边长为4,
边长为4, 分别是
分别是 上的两个动点,当
上的两个动点,当 点在
点在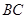 上运动时,保持
上运动时,保持 和
和 垂直,设
垂直,设 ,梯形
,梯形 的面积为
的面积为 ,下列结论
,下列结论

 ∽
∽
 的函数关系式为:
的函数关系式为:


 。
。 ①②③
①②③  ①③④
①③④  ②③④
②③④  ②④
②④