题目内容
如图，在菱形ABCD中，
，AD的垂直平分线交对角线BD于点P，垂足为E，连接CP，则
________度．
，AD的垂直平分线交对角线BD于点P，垂足为E，连接CP，则________度．72
解：先连接AP，
由四边形ABCD是菱形，∠ADC=72°，
可得∠BAD=180°-72°=108°，
根据菱形对角线的对称性可得∠ADB="1/2" ∠ADC="1/2" ×72°=36°，∠ABD=∠ADB=36度．
EP是AD的垂直平分线，由垂直平分线的对称性可得∠DAP=∠ADB=36°，
∴∠PAB=∠DAB-∠DAP=108°-36°=72度．
在△BAP中，∠APB=180°-∠BAP-∠ABP=180°-72°-36°=72度．
由菱形对角线的对称性可得∠CPB=∠APB=72度．
由四边形ABCD是菱形，∠ADC=72°，
可得∠BAD=180°-72°=108°，
根据菱形对角线的对称性可得∠ADB="1/2" ∠ADC="1/2" ×72°=36°，∠ABD=∠ADB=36度．
EP是AD的垂直平分线，由垂直平分线的对称性可得∠DAP=∠ADB=36°，
∴∠PAB=∠DAB-∠DAP=108°-36°=72度．
在△BAP中，∠APB=180°-∠BAP-∠ABP=180°-72°-36°=72度．
由菱形对角线的对称性可得∠CPB=∠APB=72度．
练习册系列答案
相关题目
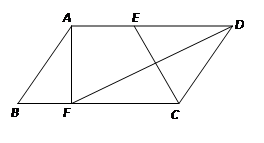
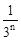
ABCD中，已知点A（﹣1，0），B（2，0），D（0，1）．则点C的坐标为 ．