题目内容
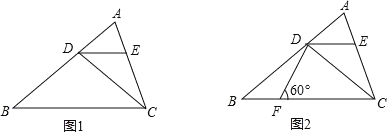
【题目】如图,AE⊥AB且AE=AB,BC⊥CD且BC=CD,那么,按照图中所标注的数据,图中实线所围成的图形面积为( ).

A.40.5B.48.5C.50D.52.5
【答案】A
【解析】
由AE⊥AB,EF⊥FH,BG⊥AG,可以得到∠EAF=∠ABG,而AE=AB,∠EFA=∠AGB,由此可以证明△AEF≌△ABG,所以AF=BG,AG=EF;同理证△BGC≌△CHD,得GC=DH,CH=BG,从而得出FH的长度,然后利用梯形DHEF的面积减去△AEF、△ABG、△BGC与△CHD的面积即可得出答案.
因为AE⊥AB,EF⊥FH,BG⊥AG,
所以∠EAF+∠BAG=∠BAG+∠ABG=90°
所以∠EAF=∠ABG
在△AEF与△ABG中
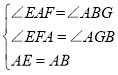
所以△AEF≌△ABG
所以AF=BG=2,AG=EF=6
因为BC⊥CD,DH⊥CH,BG⊥GC,
所以∠BCG+∠DCH=∠DCH+∠CDH=90°
所以∠BCG=∠CDH
在△BGC与△CHD中
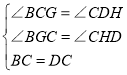
所以△BGC≌△CHD
所以GC=DH=3,CH=BG=2
所以FH=2+6+2+3=13
因为实线所围成的图形面积等于梯形DHEF的面积减去△AEF、△ABG、△BGC与△CHD的面积,
所以![]() ,
,
所以答案选A.

 阅读快车系列答案
阅读快车系列答案【题目】如图,是一种斜挎包,其挎带由双层部分、单层部分和调节扣构成.小敏用后发现,通过调节扣加长或缩短单层部分的长度,可以使挎带的长度(单层部分与双层部分长度的和,其中调节扣所占的长度忽略不计)加长或缩短.设单层部分的长度为xcm,双层部分的长度为ycm,经测量,得到如下数据:
单层部分的长度x(cm) | … | 4 | 6 | 8 | 10 | … | 150 |
双层部分的长度y(cm) | … | 73 | 72 | 71 | … |
(1)根据表中数据的规律,完成以下表格,并直接写出y关于x的函数解析式;
(2)根据小敏的身高和习惯,挎带的长度为120cm时,背起来正合适,请求出此时单层部分的长度;
(3)设挎带的长度为lcm,求l的取值范围.