题目内容
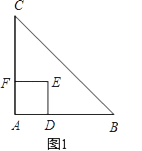
【题目】如图，在Rt△ABC中，∠C=90°，AC=6，M、N分别是边AB、AC的中点，在射线MN上取点D，使∠ADM=∠BAC，连接AD．
（1）如图1，当BC=3时，求DM的长．
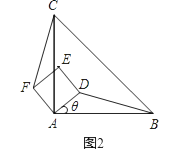
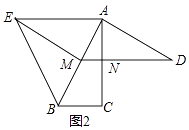
（2）如图2，以AB为底边在AB的左侧作等腰△ABE，并且使顶角∠AEB=2∠BAC，连接EM．
①判断四边形AEMD的形状，并说明理由．
②设BC=x（x＞0），四边形AEMD的面积为y，试用含x的式子表示y，并说明是否存在x的值，使得四边形AEMD的面积等于△ABC的面积？若存在，请求出x的值；若不存在，请说明理由．
【答案】
（1）
解：如图1中，
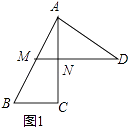
∵AM=MB，AN=NC，
∴MN∥BC，MN= 
BC= 
，
∴∠ANM=∠C=90°，
∴∠AMN+∠MAN=90°，
∵∠MAN=∠D，
∴∠AMN+∠D=90°，
∴∠MAD=90°，
∵∠ANM=∠AND=90°，∠MAN=∠D，
∴△MAN∽△ADN，
∴ 
= 
，
∴ 
= 
，
∴DN=6，
∴DM=MN+DN= +6= 
．
（2）
解：①如图2中，结论：四边形AEMD是平行四边形．
∵EA=EB，AM=BM，
∴EM⊥AB，∠MEB=∠MEA，
由（1）可知AD⊥AB，
∴EM∥AD，
∵∠AEM+∠EAM=90°，
∵∠AEB=2∠BAC，
∴∠AEM=∠BAC，
∴∠BAC+∠EAM=90°，
∴∠EAC=90°=∠MNC，
∴AE∥DM，
∴四边形AEMD是平行四边形．
②∵△MAN∽△ADN，
∴ = ，
∴ = 
，
∴DN= 
，
∴DM=MN+DN= 
+ ，
∴S四边形AEMD=DMAN=（ + ）3= x+ 
．
假设存在x，使得四边形AEMD的面积等于△ABC的面积，
则有 x+ = 
x6，
整理得x2﹣2x+36=0，
∵△=（﹣2）2﹣4×1×36＜0，
∴方程无解，假设不成立．
∴不存在使得四边形AEMD的面积等于△ABC的面积的x的值．
【解析】（1）只要证明△MAN∽△ADN，可得 = ，由此求出DN即可解决问题；（2）①结论：四边形AEMD是平行四边形．分别证明EM∥AD，AE∥DM即可；②由△MAN∽△ADN，可得 = ，即 = ，求出DN，即可解决问题．利用反证法证明不存在x的值，使得四边形AEMD的面积等于△ABC的面积；
【考点精析】解答此题的关键在于理解相似三角形的应用的相关知识，掌握测高：测量不能到达顶部的物体的高度，通常用“在同一时刻物高与影长成比例”的原理解决；测距：测量不能到达两点间的举例，常构造相似三角形求解．
