题目内容
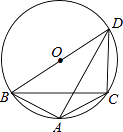
【题目】如图,AB是⊙O的直径,C是⊙O上的一点,直线MN经过点C,过点A作直线MN的垂线,垂足为点D,且∠BAC=∠DAC. 
(1)猜想直线MN与⊙O的位置关系,并说明理由;
(2)若CD=6,cos∠ACD= ![]() ,求⊙O的半径.
,求⊙O的半径.
【答案】
(1)解:直线MN与⊙O的位置关系是相切,
理由是:连接OC,
∵OA=OC,
∴∠OAC=∠OCA,
∵∠CAB=∠DAC,
∴∠DAC=∠OCA,
∴OC∥AD,
∵AD⊥MN,
∴OC⊥MN,
∵OC为半径,
∴MN是⊙O切线
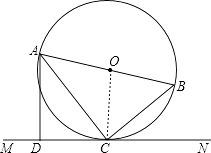
(2)解:∵CD=6,cos∠ACD= ![]() =
= ![]() ,
,
∴AC= ![]() =10,由勾股定理得:AD=8,
=10,由勾股定理得:AD=8,
∵AB是⊙O直径,AD⊥MN,
∴∠ACB=∠ADC=90°,
∵∠DAC=∠BAC,
∴△ADC∽△ACB,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴AB=12.5,
∴⊙O半径是 ![]() ×12.5=6.25
×12.5=6.25
【解析】(1)连接OC,推出AD∥OC,推出OC⊥MN,根据切线的判定推出即可;(2)求出AD、AB长,证△ADC∽△ACB,得出比例式,代入求出AB长即可.
【考点精析】关于本题考查的切线的判定定理和解直角三角形,需要了解切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线;解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法)才能得出正确答案.

【题目】用水平线和竖起线将平面分成若干个边长为1的小正方形格子,小正方形的顶点称为格点,以格点为顶点的多边形称为格点多边形.设格点多边形的面积为S,该多边形各边上的格点个数和为a,内部的格点个数为b,则S= ![]() a+b﹣1(史称“皮克公式”).
a+b﹣1(史称“皮克公式”).
小明认真研究了“皮克公式”,并受此启发对正三角形网格中的类似问题进行探究:正三角形网格中每个小正三角形面积为1,小正三角形的顶点为格点,以格点为顶点的多边形称为格点多边形,下图是该正三角形格点中的两个多边形:
根据图中提供的信息填表:
格点多边形各边上的格点的个数 | 格点多边形内部的格点个数 | 格点多边形的面积 | |
多边形1 | 8 | 1 | |
多边形2 | 7 | 3 | |
… | … | … | … |
一般格点多边形 | a | b | S |
则S与a、b之间的关系为S=(用含a、b的代数式表示).