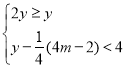ĢāÄæÄŚČŻ
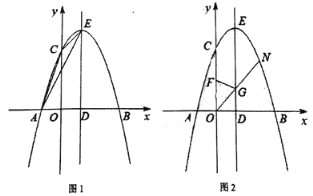
”¾ĢāÄæ”æČēĶ¼£¬Ö±Ļß![]() ”¢
”¢![]() ŹĒ½ōææijŗž²“µÄĮ½ĢõĻą»„“¹Ö±µÄ¹«Ā·£¬ĒśĻ߶Ī
ŹĒ½ōææijŗž²“µÄĮ½ĢõĻą»„“¹Ö±µÄ¹«Ā·£¬ĒśĻ߶Ī![]() ŹĒøĆŗž²“»·ŗž¹Ū¹ā“󵥵ÄŅ»²æ·Ö£®ĻÖ×¼±øŠŽ½ØŅ»ĢõÖ±ĻߊĶ¹«Ā·
ŹĒøĆŗž²“»·ŗž¹Ū¹ā“󵥵ÄŅ»²æ·Ö£®ĻÖ×¼±øŠŽ½ØŅ»ĢõÖ±ĻߊĶ¹«Ā·![]() £¬ÓĆŅŌĮ¬½ÓĮ½Ģõ¹«Ā·ŗĶ»·ŗž¹Ū¹ā“óµĄ£¬ĒŅÖ±Ļß
£¬ÓĆŅŌĮ¬½ÓĮ½Ģõ¹«Ā·ŗĶ»·ŗž¹Ū¹ā“óµĄ£¬ĒŅÖ±Ļß![]() ÓėĒśĻ߶Ī
ÓėĒśĻ߶Ī![]() ÓŠĒŅ½öÓŠŅ»øö¹«¹²µć
ÓŠĒŅ½öÓŠŅ»øö¹«¹²µć![]() £®ŅŃÖŖµć
£®ŅŃÖŖµć![]() µ½
µ½![]() ”¢
”¢![]() µÄ¾ąĄė·Ö±šĪŖ
µÄ¾ąĄė·Ö±šĪŖ![]() ŗĶ
ŗĶ![]() £¬µć
£¬µć![]() µ½
µ½![]() µÄ¾ąĄėĪŖ
µÄ¾ąĄėĪŖ![]() £¬µć
£¬µć![]() µ½
µ½![]() µÄ¾ąĄėĪŖ
µÄ¾ąĄėĪŖ![]() £®Čō·Ö±šŅŌ
£®Čō·Ö±šŅŌ![]() ”¢
”¢![]() ĪŖ
ĪŖ![]() Öį”¢
Öį”¢![]() Öį½ØĮ¢Ę½ĆęÖ±½Ē×ų±źĻµ
Öį½ØĮ¢Ę½ĆęÖ±½Ē×ų±źĻµ![]() £¬ŌņĒśĻ߶Ī
£¬ŌņĒśĻ߶Ī![]() ¶ŌÓ¦µÄŗÆŹż½āĪöŹ½ĪŖ
¶ŌÓ¦µÄŗÆŹż½āĪöŹ½ĪŖ![]() £®
£®
£Ø1£©Ēó![]() µÄÖµ£¬²¢Öø³öŗÆŹż
µÄÖµ£¬²¢Öø³öŗÆŹż![]() µÄ×Ō±äĮæµÄȔֵ·¶Ī§£»
µÄ×Ō±äĮæµÄȔֵ·¶Ī§£»
£Ø2£©ĒóÖ±Ļß![]() µÄ½āĪöŹ½£¬²¢Ēó³ö¹«Ā·
µÄ½āĪöŹ½£¬²¢Ēó³ö¹«Ā·![]() µÄ³¤¶Č(½į¹ū±£ĮōøłŗÅ)£®
µÄ³¤¶Č(½į¹ū±£ĮōøłŗÅ)£®
”¾“š°ø”æ£Ø1£©![]() £¬×Ō±äĮæµÄȔֵ·¶Ī§ĪŖ
£¬×Ō±äĮæµÄȔֵ·¶Ī§ĪŖ![]() £»£Ø2£©
£»£Ø2£©![]() £¬¹«Ā·
£¬¹«Ā·![]() µÄ³¤¶ČĪŖ
µÄ³¤¶ČĪŖ![]() £®
£®
”¾½āĪö”æ
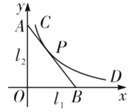
£Ø1£©ĻČČ·¶ØµćCµÄ×ų±źĪŖ£Ø1£¬8£©£¬½«Ęä“śČė![]() ¼“æÉĒó³ök=8£¬½ų¶ųČ·¶Ø×Ō±äĮæµÄȔֵ·¶Ī§£»
¼“æÉĒó³ök=8£¬½ų¶ųČ·¶Ø×Ō±äĮæµÄȔֵ·¶Ī§£»
£Ø2£©ÉčÖ±ĻßABµÄ½āĪöŹ½ĪŖy=kx+b£Øk”Ł0£©£¬½«µćP£Ø2£¬4£©“śČėµĆ4=2k+b£¬¼“b=4-2k£¬ŌņÖ±ĻßABµÄ½āĪöŹ½ĪŖy=kx+4-2k£¬øł¾ŻÖ±ĻßABÓėĒśĻ߶ĪCDÓŠĒŅ½öÓŠŅ»øö¹«¹²µćP£¬Ēó³ök=-2£¬ÄĒĆ“Ö±ĻßABµÄ½āĪöŹ½ĪŖy=-2x+8£¬ŌŁ·Ö±šĒó³öA”¢BµÄ×ų±ź£¬½ų¶ųµĆµ½ABµÄ³¤¶Č£®
½ā£ŗ£Ø1£©ÓÉĢāŅāµĆ£ŗµć![]() µÄ×ų±źĪŖ
µÄ×ų±źĪŖ![]() £¬½«Ęä“śČė
£¬½«Ęä“śČė![]() µĆ£ŗ
µĆ£ŗ![]() £¬
£¬
![]() ĒśĻ߶Ī
ĒśĻ߶Ī![]() µÄŗÆŹż½āĪöŹ½ĪŖ
µÄŗÆŹż½āĪöŹ½ĪŖ![]() £¬
£¬
![]() µć
µć![]() µÄ×ų±źĪŖ
µÄ×ų±źĪŖ![]()
”ą×Ō±äĮæµÄȔֵ·¶Ī§ĪŖ![]() £»
£»
£Ø2£©ÉčÖ±Ļß![]() µÄ½āĪöŹ½ĪŖ
µÄ½āĪöŹ½ĪŖ![]() £¬
£¬
ÓÉ£Ø1£©Ņ×ĒóµĆµć![]() µÄ×ų±źĪŖ
µÄ×ų±źĪŖ![]() £¬
£¬
![]() £¬¼“
£¬¼“![]() £¬
£¬
![]() Ö±Ļß
Ö±Ļß![]() µÄ½āĪöŹ½ĪŖ
µÄ½āĪöŹ½ĪŖ![]() £¬
£¬
ĮŖĮ¢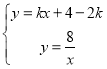 £¬µĆ
£¬µĆ![]() £¬
£¬
![]() £¬
£¬
![]() ÓÉĢāŅāµĆ£ŗ
ÓÉĢāŅāµĆ£ŗ![]() £¬½āµĆ
£¬½āµĆ![]() £¬
£¬
![]() Ö±Ļß
Ö±Ļß![]() µÄ½āĪöŹ½ĪŖ
µÄ½āĪöŹ½ĪŖ![]() £¬µ±
£¬µ±![]() Ź±£¬
Ź±£¬![]() £»µ±
£»µ±![]() Ź±£¬
Ź±£¬![]() £¬
£¬
¼“![]() ”¢
”¢![]() µÄ×ų±ź·Ö±šĪŖ
µÄ×ų±ź·Ö±šĪŖ![]() £¬
£¬![]() £¬
£¬
![]() £®
£®
![]() ¹«Ā·
¹«Ā·![]() µÄ³¤¶ČĪŖ
µÄ³¤¶ČĪŖ![]() £®
£®

”¾ĢāÄæ”æijĖ®¹ūµź¼Ę»®½ųA£¬BĮ½ÖÖĖ®¹ū¹²140Ē§æĖ£¬ÕāĮ½ÖÖĖ®¹ūµÄ½ų¼ŪŗĶŹŪ¼ŪČē±ķĖłŹ¾
½ų¼Ū | ŹŪ¼Ū | |
AÖÖĖ®¹ū | 5 | 8 |
BÖÖĖ®¹ū | 9 | 13 |
![]() ČōøĆĖ®¹ūµź¹ŗ½ųÕāĮ½ÖÖĖ®¹ū¹²»Ø·Ń1020ŌŖ£¬ĒóøĆĖ®¹ūµź·Ö±š¹ŗ½ųA£¬BĮ½ÖÖĖ®¹ūø÷¶ąÉŁĒ§æĖ£æ
ČōøĆĖ®¹ūµź¹ŗ½ųÕāĮ½ÖÖĖ®¹ū¹²»Ø·Ń1020ŌŖ£¬ĒóøĆĖ®¹ūµź·Ö±š¹ŗ½ųA£¬BĮ½ÖÖĖ®¹ūø÷¶ąÉŁĒ§æĖ£æ
![]() ŌŚ
ŌŚ![]() µÄ»ł“”ÉĻ£¬ĪŖĮĖÓ½Ó“ŗ½ŚµÄĄ“ĮŁ£¬Ė®¹ūµźĄĻ°å¾ö¶Ø°ŃAÖÖĖ®¹ūČ«²æ°ĖÕŪ³öŹŪ£¬BÖÖĖ®¹ūČ«²æ½µ¼Ū
µÄ»ł“”ÉĻ£¬ĪŖĮĖÓ½Ó“ŗ½ŚµÄĄ“ĮŁ£¬Ė®¹ūµźĄĻ°å¾ö¶Ø°ŃAÖÖĖ®¹ūČ«²æ°ĖÕŪ³öŹŪ£¬BÖÖĖ®¹ūČ«²æ½µ¼Ū![]() ³öŹŪ£¬ÄĒĆ“ŹŪĶźŗó¹²»ńĄū¶ąÉŁŌŖ£æ
³öŹŪ£¬ÄĒĆ“ŹŪĶźŗó¹²»ńĄū¶ąÉŁŌŖ£æ