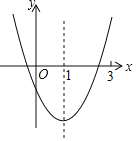题目内容
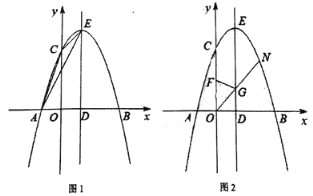
【题目】如图1,抛物线![]() 与x轴相交于点A、点B,与y轴交于点C(0,3),对称轴为直线x=1,交x轴于点D,顶点为点E.
与x轴相交于点A、点B,与y轴交于点C(0,3),对称轴为直线x=1,交x轴于点D,顶点为点E.
(1)求该抛物线的解析式;
(2)连接AC,CE,AE,求△ACE的面积;
(3)如图2,点F在y轴上,且OF=![]() ,点N是抛物线在第一象限内一动点,且在抛物线对称轴右侧,连接ON交对称轴于点G,连接GF,若GF平分∠OGE,求点N的坐标.
,点N是抛物线在第一象限内一动点,且在抛物线对称轴右侧,连接ON交对称轴于点G,连接GF,若GF平分∠OGE,求点N的坐标.
【答案】(1)y=-x2+2x+3;(2)1;(3)点N的坐标为:(![]() ,
,![]() ).
).
【解析】
(1)由点C的坐标,求出c,再由对称轴为x=1,求出b,即可得出结论;
(2)先求出点A,E坐标,进而求出直线AE与y轴的交点坐标,最后用三角形面积公式计算即可得出结论;
(3)先利用角平分线定理求出FQ=1,进而利用勾股定理求出OQ=1=FQ,进而求出∠BON=45°,求出直线ON的解析式,最后联立抛物线解析式求解,即可得出结论.
解:(1)∵抛物线y=-x2+bx+c与y轴交于点C(0,3),
令x=0,则c=3,
∵对称轴为直线x=1,
∴![]() ,
,
∴b=2,
∴抛物线的解析式为y=-x2+2x+3;
(2)如图1, AE与y轴的交点记作H,
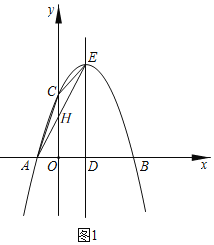
由(1)知,抛物线的解析式为y=-x2+2x+3,
令y=0,则-x2+2x+3=0,
∴x=-1或x=3,
∴A(-1,0),
当x=1时,y=-1+2+3=4,
∴E(1,4),
∴直线AE的解析式为y=2x+2,
∴H(0,2),
∴CH=3-2=1,
∴S△ACE=![]() CH|xE-xA|=
CH|xE-xA|=![]() ×1×2=1;
×1×2=1;
(3)如图2, 过点F作FP⊥DE于P,则FP=1,过点F作FQ⊥ON于Q,
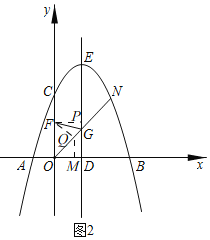
∵GF平分∠OGE,
∴FQ=FP=1,
在Rt△FQO中,OF=![]() ,
,
根据勾股定理得,OQ=![]() ,
,
∴OQ=FQ,
∴∠FOQ=45°,
∴∠BON=90°-45°=45°,
过点Q作QM⊥OB于M,OM=QM
∴ON的解析式为y=x①,
∵点N在抛物线y=-x2+2x+3②上,
联立①②,则![]() ,
,
解得: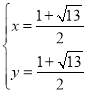 或
或 (由于点N在对称轴x=1右侧,所以舍去),
(由于点N在对称轴x=1右侧,所以舍去),
∴点N的坐标为:(![]() ,
,![]() ).
).

 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案