题目内容
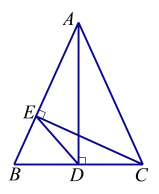
【题目】如图,⊙O中的弦BC等于⊙O的半径,延长BC到D,使BC=CD,点A为优弧BC上的一个动点,连接AD,AB,AC,过点D作DE⊥AB,交直线AB于点E,当点A在优弧BC上从点C运动到点B时,则DE+AC的值的变化情况是( )
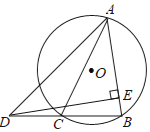
A.不变B.先变大再变小C.先变小再变大D.无法确定
【答案】B
【解析】
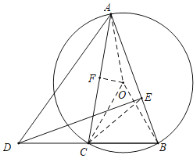
如图,连接OA,OC,OB,EC,作OF⊥AC于F,根据直角三角形斜边中线的性质可得EC=CD=CB,根据等腰三角形的性质可得∠CBE=∠CEB,∠AOF=∠COF,根据圆周角定理可得∠AOC=2∠ABC,利用外角性质可得∠DCE=2∠CBE,即可证明∠AOC=∠DCE,利用SAS可证明△AOC≌△DCE,可得AC=DE,即可得出DE+AC=2AC,根据AC的变化即可得答案.
如图,连接OA,OC,OB,EC,作OF⊥AC于F.
∵DE⊥AB,
∴∠DEB=90°,
∵DC=BC,
∴EC=CD=CB,
∵BC=OC=OB=OA,CD=BC,
∴OA=OC=CD=CE=CB,
∴∠CBE=∠CEB,
∵OF⊥AC,OA=OC,
∴∠AOF=∠COF,
∵∠AOC=2∠ABC,∠DCE=∠CEB+∠CBE=2∠CBE,
∴∠AOC=∠DCE,
∴△AOC≌△DCE(SAS),
∴AC=DE,
∴AC+DE=2AC,
观察图象可知AC的值先变大再变小,
故AC+DE的值先变大再变小,
故选B.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目