Question

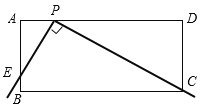
【题目】如图，在矩形ABCD中，AB=4，AD=10．直角尺的直角顶点P在AD上滑动时（点P与A,D不重合），一直角边经过点C，另一直角边AB交于点E．

（1）求证：

（2）是否存在这样的点P，使的周长等于周长的2倍？若存在，求出DP的长；若不存在，请说明理由．

Answer 1

【答案】（1）见解析；（2）存在这样的点P，使的周长等于周长的2倍；DP的长为8.

【解析】

（1）首先根据余角的等量转化，得出∠CPD=∠AEP，∠APE=∠DCP，然后根据两角对应相等，两个三角形相似，即可判定；

（2）首先假设存在这样的点，然后根据相似的性质得出CD：AP=PD：AE=2，即可得解.

（1）∵∠CPD=90°-∠APE=∠AEP，

∴∠CPD=∠AEP，∠APE=∠DCP．

∴（两角对应相等，两个三角形相似）

（2）假设存在这样的点P，

∵Rt△AEP∽Rt△DPC，

∴CD：AP=PD：AE=2．

又∵CD=AB=4，

∴AP=2，PD=8，

∴存在这样的P点，且DP长为8．