题目内容
【题目】如图,平行四边形ABCD中,BC=2AB=4,∠ABC=60°,PA⊥AD,E,F分别为BC,PE的中点,AF⊥平面PED. 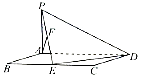
(1)求证:PA⊥平面ABCD;
(2)求直线BF与平面AFD所成角的正弦值.
【答案】
(1)解:连接AE,
∵AF⊥平面PED,ED平面PED,
∴AF⊥ED,
在平行四边形ABCD中,BC=2AB=4,∠ABC=60°,
∴AE=2, ![]() ,
,
∴AE2+ED2=AD2,∴AE⊥ED,
又∵AF∩AE=A,AF平面PAE,PA平面PAE,
∴ED⊥平面PAE,∵PA平面PAE,
∴ED⊥PA,
又PA⊥AD,AD∩ED=D,AE平面ABCD,AD平面ABCD,
∴PA⊥平面ABCD

(2)解:以E为坐标原点,以EA,ED为x轴,y轴建立如图所示的空间直角坐标系,
则A(0,2,0), ![]() ,
, ![]() ,
,
∵AF⊥平面PED,所以AF⊥PE,
又F为PE中点,∴PA=AE=2,
∴P(0,2,2),F(0,1,1),
∴ ![]() ,
, ![]() ,
, ![]() ,
,
设平面AFD的法向量为 ![]() ,
,
由 ![]() ,
, ![]() 得,
得, ![]() ,
,
令x=1,得 ![]() .
.
设直线BF与平面AFD所成的角为θ,则: 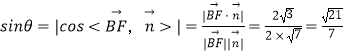 ,
,
即直线BF与平面AFD所成角的正弦值为 ![]() .
.

【解析】(1)利用勾股定理的逆定理得出AE⊥DE,由AF⊥平面PED得DE⊥AF,故而DE⊥平面PAE,于是DE⊥PA,结合PA⊥AD得出PA⊥平面ABCD;(2)以E为原点建立空间坐标系,求出平面ADF的法向量 ![]() ,则|cos<
,则|cos< ![]() >|为直线BF与平面AFD所成角的正弦值.
>|为直线BF与平面AFD所成角的正弦值.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目


