题目内容
【题目】(1)若|x+5|=2,则x= ;
(2)代数式|x﹣1|+|x+3|的最小值为 ,当取此最小值时,x的取值范围是 ;
(3)解方程:|2x+4|﹣|x﹣3|=9.
【答案】(1)﹣3或﹣7;(2)4,﹣3≤x≤1;(3)x=﹣16或x=![]() .
.
【解析】试题分析:(1)解绝对值方程.
(2)数形结合,利用绝对值的意义在数轴上求最小值.
(3)分类讨论,化简绝对值,解绝对值方程.
【解答】试题分析:
试题解析:
解:(1)∵|x+5|=2,
∴x+5=2或x+5=﹣2,
解得:x=﹣3或x=﹣7.
(2)由数形结合得,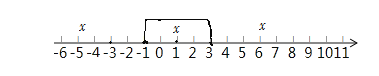
代数式|x﹣1|+|x+3|的最小值为1﹣(﹣3)=4,当取此最小值时,x的取值范围是﹣3≤x≤1.
(3)当x≤﹣2时,原方程可化为:﹣2x﹣4+x﹣3=9,
解得:x=﹣16,
当x≥3时,原方程可化为:2x+4﹣x+3=9,
解得:x=2
与x≥3不符;
当﹣2<x<3时,原方程可化为:2x+4+x﹣3=9,
解得:x=![]() .
.
综上所述,方程的解为:x=﹣16或x=![]() .
.
故答案为:﹣3或﹣7;4,﹣3≤x≤1.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目