题目内容
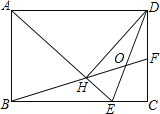
【题目】一次数学课上，老师在黑板上画了如图图形，并写下了四个等式：
①BD=CA，②AB=DC，③∠B=∠C，④∠BAE=∠CDE．
要求同学从这四个等式中选出两个作为条件，推出AE=DE．请你试着完成老师提出的要求，并说明理由．（写出一种即可）
已知：____（请填写序号），求证：AE=DE．
证明：
【答案】①BD=CA，②AB=DC，
【解析】试题分析：
本题的选择方式有多种：（1）可由①BD=CA，②AB=DC结合AD是公共边证△ABD≌△DCA，可得∠ADE=∠DAE，再由“等角对等边”得到AE=DE；（2）可由②AB=DC，③∠B=∠C结合∠AEB=∠DEC，证△ABE≌△DCE，可得AE=DE；（3）可由②AB=DC，④∠BAE=∠CDE结合∠AEB=∠DEC，证△ABE≌△DCE，可得AE=DE；
试题解析：
已知：②AB=DC，③∠B=∠C，求证：AE=DE，
证明：在△ABE和△DCE中：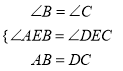 
，
∴△ABE≌△DCE（AAS）,
∴ AE=DE.
练习册系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
