Question

【题目】抛物线y=（x﹣3）（x+1）与x轴交于A，B两点（点A在点B左侧），与y轴交于点C，点D为顶点．

（1）求点B及点D的坐标．

（2）连结BD，CD，抛物线的对称轴与x轴交于点E．

①若线段BD上一点P，使∠DCP=∠BDE，求点P的坐标．

②若抛物线上一点M，作MN⊥CD，交直线CD于点N，使∠CMN=∠BDE，求点M的坐标．

Answer 1

【答案】（1）（1，﹣4）；（2）点M坐标为（，﹣）或（5，12）．

【解析】试题分析：（1）解方程求出或 抛物线与轴交于两点（点A在点B左侧），确定点的坐标为 将配方，写成顶点式为即可确定顶点 的坐标；
（2）①根据抛物线得到点C、点E的坐标．连接BC，过点C作于H，由勾股定理得出证明为直角三角形．

分别延长与轴相交于点 根据两角对应相等的两三角形相似证明 得出运用待定系数法求出直线CQ的解析式为y=-直线BD的解析式为解方程组即可求出点P的坐标；
②分两种情况进行讨论：（Ⅰ）当点M在对称轴右侧时．若点N在射线CD上，如备用图1，延长MN交y轴于点F，过点M作轴于点G，先证明由相似三角形对应边成比例得出．设，再证明均为等腰直角三角形，然后用含的代数式表示点M的坐标，将其代入抛物线求出的值，得到点M的坐标；若点N在射线DC上，同理可求出点M的坐标；（Ⅱ）当点M在对称轴左侧时．由于得到 根据直角三角形两锐角互余得出 而抛物线左侧任意一点K，都有 所以点M不存在．

试题解析：

（1）∵抛物线与轴交于两点（点A在点B左侧），

∴当时，

解得或

∴点B的坐标为

∴顶点D的坐标为

（2）①如右图．

∵抛物线与与y轴交于点C，

∴C点坐标为

∵对称轴为直线

∴点E的坐标为

连接BC，过点C作于H，则H点坐标为

为直角三角形．

分别延长与轴相交于点

即

∴直线CQ的解析式为

直线BD的解析式为

由方程组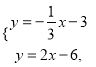 解得 ．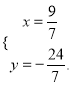

∴点P的坐标为

②（Ⅰ）当点M在对称轴右侧时．

若点在射线上，如备用图1，延长MN交轴于点F，过点M作轴于点．

设 则

均为等腰直角三角形，

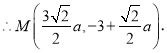
代入抛物线解得

若点N在射线DC上，如备用图2，MN交y轴于点F，过点M作轴于点G．

设 则

均为等腰直角三角形，

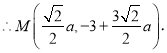
代入抛物线解得

代入抛物线，解得

（Ⅱ）当点M在对称轴左侧时．

而抛物线左侧任意一点K，都有

∴点M不存在．

综上可知，点M坐标为或