题目内容
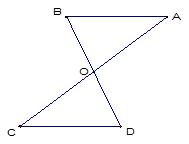
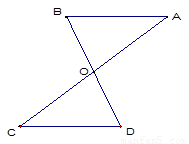
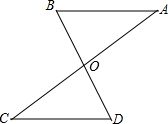 已知:如图,AC与BD交于点O,AO=CO,BO=DO.
已知:如图,AC与BD交于点O,AO=CO,BO=DO.
求证:AB∥CD.
证明:在△AOB和△COD中,
∵ ,
,
∴△AOB≌△COD(SAS),
∴∠A=∠C,
∴AB∥CD.
分析:由已知两对边相等,再加上一对对顶角相等,利用SAS得出△AOB≌△COD,利用全等三角形的对应角相等得到一对内错角相等,利用内错角相等两直线平行,可得出AB与CD平行.
点评:此题考查了全等三角形的判定与性质,以及平行线的判定,全等三角形的判定方法有:SSS;SAS;ASA;AAS,以及HL(直角三角形判定全等的方法).
∵
 ,
,∴△AOB≌△COD(SAS),
∴∠A=∠C,
∴AB∥CD.
分析:由已知两对边相等,再加上一对对顶角相等,利用SAS得出△AOB≌△COD,利用全等三角形的对应角相等得到一对内错角相等,利用内错角相等两直线平行,可得出AB与CD平行.
点评:此题考查了全等三角形的判定与性质,以及平行线的判定,全等三角形的判定方法有:SSS;SAS;ASA;AAS,以及HL(直角三角形判定全等的方法).

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案
相关题目
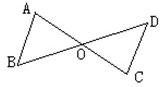 22、已知,如图,AC与BD交于点O,AO=OC,BO=DO.求证:AB∥CD.
22、已知,如图,AC与BD交于点O,AO=OC,BO=DO.求证:AB∥CD. (2012•温州二模)已知:如图,AC与BD交于点O,AO=CO,BO=DO.
(2012•温州二模)已知:如图,AC与BD交于点O,AO=CO,BO=DO.