��Ŀ����
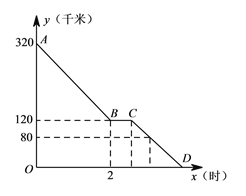
����Ŀ����ͼ���߶�AB��A��2��3����B��5��3����������y������x��1��2��m2+2m+1��x�����������ֱ�ΪC��D����C�ڵ�D����ࣩ
��1����mΪ��ֵʱ�����߹�ԭ�㣬�������ʱ�����ߵĽ���ʽ���Գ����������꣮
��2���������ߵĶ���ΪP��mΪ��ֵʱ��PCD���������������Ƕ��٣�
��3�����߶�AB��y������ƽ��n����λ����m��n�������Ĺ�ϵʱ���������ܰ��߶�AB�ֳ�1��2�����֣�
���𰸡���1����m��0��m��2ʱ�������߹�ԭ�㣬��ʱ�����ߵĽ���ʽ��y������x��1��2+1���Գ���Ϊֱ��x��1������Ϊ��1��1������2��mΪ1ʱ��PCD����������������2![]() ����3��n��m2��2m+6��n��m2��2m+11��
����3��n��m2��2m+6��n��m2��2m+11��
��������
��1�����������߹�ԭ�����Ŀ�еĺ�������ʽ�������m��ֵ���������ʱ�����ߵĽ���ʽ���Գ����������ꣻ
��2��������Ŀ�еĺ�������ʽ�Ͷ��κ��������ʣ��������mΪ��ֵʱ��PCD����������õ�C��D�����꣬�ɴ������PCD��������ֵ��
��3�����������������ܰ��߶�AB�ֳ�1��2����������������������������߶�AB�������ߵĽ��㣬���ɵõ���m��n�������Ĺ�ϵʱ���������ܰ��߶�AB�ֳ�1��2�����֣�
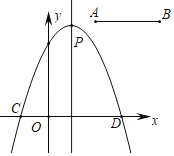
��1����y������x��1��2��m2+2m+1��ԭ�㣨0��0��ʱ��0����1��m2+2m+1����m1��0��m2��2��
��m1��0ʱ��y������x��1��2+1��
��m2��2ʱ��y������x��1��2+1��
���Ͽɵã���m��0��m��2ʱ�������߹�ԭ�㣬��ʱ�����ߵĽ���ʽ��y������x��1��2+1���Գ���Ϊֱ��x��1������Ϊ��1��1����
��2����������y������x��1��2��m2+2m+1��
��������ߵĶ���PΪ��1����m2+2m+1����
����m2+2m+1���ʱ����PCD��������
�ߩ�m2+2m+1������m��1��2+2��
�൱m��1ʱ����m2+2m+1���Ϊ2��
��y������x��1��2+2��
��y��0ʱ��0������x��1��2+2����x1��1+![]() ��x2��1��
��x2��1��![]() ��
��
���C��������1��![]() ��0������D��������1+
��0������D��������1+![]() ��0��
��0��
��CD����1+![]() ������1��
������1��![]() ����2
����2![]() ��
��
��S��PCD��![]() ��2
��2![]() ��
��
��mΪ1ʱ��PCD����������������2![]() ��
��
��3�����߶�AB��y������ƽ��n����λA��2��3��n����B��5��3��n��
���߶�AB�ֳ�1��2�����֣���㣨3��3��n����4��3��n���ڸ������߽���ʽ�ϣ�
�ѣ�3��3��n�����������߽���ʽ�ã�
3��n������3��1��2��m2+3m+1��
��n��m2��2m+6��
�ѣ�4��3��n�����������߽���ʽ����
3��n������3��1��2��m2+3m+1��
��n��m2��2m+11��
��n��m2��2m+6��n��m2��2m+11��

����Ŀ��ij�̳���������ʱ������ij��������Ʒ�����г����飬����Ʒ�ĵ�![]() ��Ľ���
��Ľ���![]() (Ԫ����)��
(Ԫ����)��![]() (��)֮��������Ϣ���±���
(��)֮��������Ϣ���±���
ʱ�� |
|
|
���� |
| 40 |
����Ʒ�����۹����У�������![]() (��)��
(��)��![]() (��)֮��ĺ�����ϵ��ͼ��ʾ��
(��)֮��ĺ�����ϵ��ͼ��ʾ��
�����۹����У��̳�ÿ�����۵ĸò�Ʒ��ÿ��80Ԫ�ļ۸�ȫ���۳���
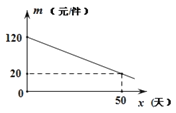
��1�������Ʒ��������![]() (��)��
(��)��![]() (��)֮��ĺ�����ϵ��
(��)֮��ĺ�����ϵ��
��2�����![]() ����̳����۸���Ʒ��õ�����Ϊ
����̳����۸���Ʒ��õ�����Ϊ![]() Ԫ�����
Ԫ�����![]() ��
��![]() ֮��ĺ�����ϵʽ��������ڼ����������������������Ƕ���Ԫ��
֮��ĺ�����ϵʽ��������ڼ����������������������Ƕ���Ԫ��
��3�������۹����У����������������2400Ԫ�Ĺ��ж����죿
����Ŀ��Ϊ�����л����㴫ͳ�Ļ���ijУ��֯������ʫ����֪ʶ�������ɾ��꼶��������ѧ���μ�ѡ����������ѡ��10����ʤ�ߣ������ǶԲ���ѧ���ɼ��IJ�����ͳ�ƣ�
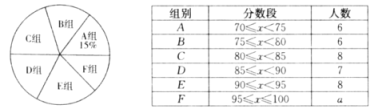
��1��ͳ�Ʊ��У�![]() =_____��������������λ����_____��ͳ��ͼ�У�
=_____��������������λ����_____��ͳ��ͼ�У�![]() ���������ε�Բ�Ľ���_____����
���������ε�Բ�Ľ���_____����
��2������ͬѧ����88�֣���˵�Լ��ڲμ�ѡ������ͬѧ����������ƫ��ˮƽ������Ϊ��˵���е�����Ϊʲô��
��3��ѡ����10����ʤ���У�������Ů���ķֲ�������±���
һ�� | ���� | ���� | �İ� | ��� | ���� | |
�������� | 1 | 1 | 2 | 1 | 0 | 0 |
������ | 1 | 0 | 0 | 2 | 1 | 1 |
��������ѡ1��������1��Ů������ѧУ�μ�ȫ���ı����������б�������״ͼ����������Ů���������İ�ĸ��ʣ�