题目内容
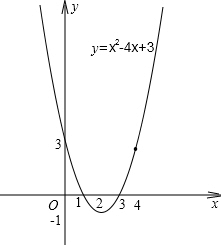
对于抛物线y=x2-4x+3，
（1）与y轴的交点坐标是
（2）利用描点法画出函数的图象．
（1）与y轴的交点坐标是
（0，3）
（0，3）
，与x轴交点坐标是（1，0）；（3，0）
（1，0）；（3，0）
，顶点坐标是（2，-1）
（2，-1）
；（2）利用描点法画出函数的图象．
分析：（1）令x=0，即可求出函数与y轴的交点坐标，令y=0，即可求出与x轴的交点坐标，配方之后即可求出函数的顶点坐标．
（2）找到对称轴两侧的关键点及顶点坐标，即可画出函数图象．
（2）找到对称轴两侧的关键点及顶点坐标，即可画出函数图象．
解答：解：（1）当x=0时，y=3，则与y轴的交点坐标为（0，3）；
当y=0时，x2-4x+3=0，
解得，（x-1）（x-3）=0，
x1=1，x2=3，
则与x轴的交点坐标为（1，0），（3，0）；
原式可化为y=x2-4x+4-1=（x-2）2-1，
其顶点坐标为（2，-1）．
（2）列表
描点、连线
当y=0时，x2-4x+3=0，
解得，（x-1）（x-3）=0，
x1=1，x2=3，
则与x轴的交点坐标为（1，0），（3，0）；
原式可化为y=x2-4x+4-1=（x-2）2-1，
其顶点坐标为（2，-1）．
（2）列表
| X | 0 | 1 | 2 | 3 | 4 |
| y=x2-4x+3 | 3 | 0 | -1 | 0 | 3 |
点评：本题考查了抛物线与x轴的交点坐标，二次函数的图象与二次函数的画法，要对二次函数有一个明确的认识方可正确解答．
练习册系列答案
口算心算速算应用题系列答案
同步拓展阅读系列答案
相关题目
对于抛物线y=x2-3，下列说法中正确的是（ ）
| A、抛物线的开口向下 | B、顶点（0，-3）是抛物线的最低点 | C、顶点（0，-3）是抛物线的最高点 | D、抛物线在直线x=0右侧的部分下降的 |
对于抛物线 y=x2-4x+3．
（1）它与x轴交点的坐标为 ，与y轴交点的坐标为 ，顶点坐标为 ；
（2）在坐标系中利用描点法画出此抛物线；
（3）利用以上信息解答下列问题：若关于x的一元二次方程x2-4x+3-t=0（t为实数）在-1＜x＜
的范围内有解，则t的取值范围是 ．
（1）它与x轴交点的坐标为
（2）在坐标系中利用描点法画出此抛物线；
| x | … | … | |||||
| y | … | … |
（3）利用以上信息解答下列问题：若关于x的一元二次方程x2-4x+3-t=0（t为实数）在-1＜x＜
| 7 |
| 2 |