题目内容
对于抛物线 y=x2-4x+3．（1）它与x轴交点的坐标为
（2）在坐标系中利用描点法画出此抛物线；
| x | … | … | |||||
| y | … | … |
（3）利用以上信息解答下列问题：若关于x的一元二次方程x2-4x+3-t=0（t为实数）在-1＜x＜
| 7 |
| 2 |
分析：运用二次函数与x轴相交时，y=0，与y轴相交时，x=0，即可求出，用公式法可求出顶点坐标，利用列表，描点，连线可画出图象．
解答：解：（1）它与x轴交点的坐标为：（-1，0）（-3，0），与y轴交点的坐标为（0，3），顶点坐标为（2，-1）；
故答案为：（1，0）（3，0），（0，3）（2，-1）
（2）列表：
图象如图所示．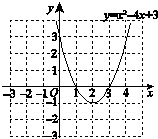
（3）∵关于x的一元二次方程x2-4x+3-t=0（t为实数）在-1＜x＜
的范围内有解，
∵y=x2-4x+3的顶点坐标为（2，-1），
若x2-4x+3-t=0有解，方程有两个根，则：b2-4ac=16-4（3-t）≥0，解得：-1≤t
当x=-1，代入x2-4x+3-t=0，t=8，
当x=
，代入x2-4x+3-t=0，t=
，
∵x＞-1，∴t＜8，
∴t的取值范围是：-1≤t＜8，
故填：-1≤t＜8
故答案为：（1，0）（3，0），（0，3）（2，-1）
（2）列表：
| x | … | 0 | 1 | 2 | 3 | 4 | … |
| y | … | 3 | 0 | -1 | 0 | 3 | … |
（3）∵关于x的一元二次方程x2-4x+3-t=0（t为实数）在-1＜x＜
| 7 |
| 2 |
∵y=x2-4x+3的顶点坐标为（2，-1），
若x2-4x+3-t=0有解，方程有两个根，则：b2-4ac=16-4（3-t）≥0，解得：-1≤t
当x=-1，代入x2-4x+3-t=0，t=8，
当x=
| 7 |
| 2 |
| 5 |
| 4 |
∵x＞-1，∴t＜8，
∴t的取值范围是：-1≤t＜8，
故填：-1≤t＜8
点评：此题主要考查了二次函数与坐标轴的交点求法，以及用描点法画二次函数图象和结合图象判定一元二次方程的解的情况．
练习册系列答案
相关题目
对于抛物线y=x2-3，下列说法中正确的是（ ）
| A、抛物线的开口向下 | B、顶点（0，-3）是抛物线的最低点 | C、顶点（0，-3）是抛物线的最高点 | D、抛物线在直线x=0右侧的部分下降的 |