题目内容
【题目】某校学生骑自行车从学校去某地植树，过了一段时间学校派后勤人员开车去送树苗和植树工具，学生、后勤人员离开学校的距离y（千米）与行驶时间x（分钟）的函数图象如图所示．
（1）根据图中信息，求学生骑自行车的速度和后勤人员开车的速度；
（2）说出B点的意义并求出B点的坐标；
（3）请你直接写出学生队伍与后勤人员都在运动中相距3千米的时间．
【答案】（1）学生骑自行车的速度为36千米/小时，后勤人员开车的速度90千米/小时；（2）B点的坐标为（10，6），B点的意义为后勤人员开车出发10分钟后和学生骑自行车相遇；（3）当x=
或
时，学生队伍与后勤人员在运动中相距3千米.
【解析】试题分析：
（1）由图中信息可知，学生30分钟骑行了18千米，后勤人员开车12分钟行驶了18千米；由此可计算出他们各自的速度；
（2）先分别根据图中所获取的信息求出线段OD和AC的解析式，再把两个解析式联立得方程组，解方程组可求得点B的坐标；点B的意义是“点B的横坐标和纵坐标分别表示在什么时间，距学校多远处，后勤人员追上学生队伍”；
（3）分学生队伍和后勤人员在相遇前和相遇后两种情况下相距3km，分别列方程解答即可；
试题解析：
（1）由图象可知，学校到植树地的距离为18千米，学生骑自行车用30分钟到达，后勤人员开车用18﹣6=12分钟到达，30分钟=0.5小时，12分钟=0.2小时，
∴学生骑自行车的速度为：18÷0.5=36（千米/小时），
后勤人员开车的速度：18÷0.2=90（千米/小时）．
（2）设线段OD的解析式为y=kx，（0≤x≤30）
把（30，18）代入y=kx得：30k=18，
解得：k=0.6，
∴线段OD的解析式为y=0.6x（0≤x≤30），
设线段AC的解析式为y=k1x+B，（0≤x≤30）
把（18，18），（6，0）代入y=kx得：
解得：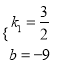 
，
∴线段AC的解析式为
，
联立线段OD的解析式：y=0.6x（0≤x≤30）和线段AC的解析式： 
，
得： 
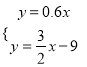，解得： 
.
∴B点的坐标为（10，6），
B点的意义为：后勤人员在学生队伍出发10分钟后和学生队伍相遇，此时距学校6km．
（3）当6＜x≤10时，学生队伍与后勤人员在运动中相距3千米，可得： 
，解得： 
；
当10＜x≤18时，学生队伍与后勤人员在运动中相距3千米，可得：
，解得： 
.
综上所述，当学生队伍出发
小时和
小时时，后勤人员和学生队伍相遇.
