��Ŀ����
����Ŀ����ͼ����ֱ������ABCD�У�AD // BC����B��90�㣬AD��24cm��BC��26cm������P��A�㿪ʼ��AD����D��3cm/s���ٶ��˶�������Q�ӵ�C��ʼ��CB�������1cm/s���ٶ��˶�����P��Q�ֱ��A��Cͬʱ���������˶�ʱ��Ϊt (s)��������һ�㵽��˵�ʱ����һ��Ҳ��ֹ֮ͣ�˶���

�ٵ�tΪ��ֵʱ����CD��PQΪ���ߣ������εĵף�AD��BC����һ���֣���ȫ����Ϊ�������ܹ���һ�������Σ�
�������tΪ��ֵʱ���ı���PQCDΪ�������Ρ�
���𰸡���1��t=0��t=8;(2) t=7
�����������������(1)CD��PQΪ�߹��������������Ա����������߶ζ˵����������Է�����������P,A;C,Q�غϣ�P,D�غ�.
(2) ����P��PF��BC�ڵ�F������D��DE��BC�ڵ�E,Ҫ���ɵ��������Σ�����![]() PQFȫ��
PQFȫ��![]() BCE.
BCE.
���������
�ٸ�������ã�
����P���A�غ�ʱ�ܹ���һ�������Σ���ʱt=0��
�ߵ�P����D���裺8(s)��
��Q����B���裺26(s)��
�൱��P���D�غ�ʱ�ܹ���һ�������Σ���ʱt=8s��
�ʵ�t=0��8sʱ,��CD��PQΪ����,�����εĵ�(AD��BC)��һ����(��ȫ��)Ϊ�������ܹ���һ��������.
�ڡ�BCAD=2cm��
����P��PF��BC�ڵ�F������D��DE��BC�ڵ�E��
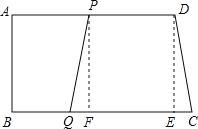
�ߵ�PQ=CDʱ���ı���PQCDΪ�������Σ�
����PFQ����DCE��EF=PD��
��QF=CE=2cm��
�൱CQPD=QF+CE=4cmʱ���ı���PQCDΪ�������Σ�
��t(243t)=4��
��t=7(s)��
�൱t=7sʱ���ı���PQCDΪ��������.





