题目内容
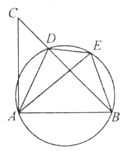
【题目】如图，在⊙O中，AB是直径，CD是弦，AB⊥CD，垂足为E，连结CO，AD，∠BAD＝20°，则下列说法中正确的是( )
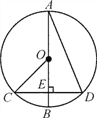
A. ∠BOC＝2∠BAD B. CE＝EO C. ∠OCE＝40° D. AD＝2OB
【答案】A
【解析】
根据“垂径定理”和“圆的有关性质”进行分析即可即可.
如下图，连接OD，
∵在⊙O中，AB是直径，CD是弦，AB⊥CD，垂足为E，
∴∠OEC=90°，
，
∴∠BOC=∠BOD，
∵∠BOD=2∠BAD=40°，
∴∠BOC=2∠BAD=40°，即A中结论正确；
∴∠OCE=180°-90°-40°=50°，即C中结论不成立；
∴∠COE
∠OCE，
∴CEEO，即B中结论不成立；
∵AB是⊙O的直径，而AD是⊙O的一条非直径的弦，
∴AB>AD，
∵AB=2OB，
∴AD<2OB，即D中结论不成立.
综上所述，上述四个选项中，只有A中的结论成立.
故选A.
点睛；熟悉“垂径定理和圆的相关性质”是解答本题的关键.
练习册系列答案
阳光课堂课时作业系列答案
相关题目
