题目内容

已知：如图，点E为正方形ABCD的边BC上一点，连结AE，过点D作DG⊥AE，垂足为G，延长DG交AB于点F。求证：DF=AE。
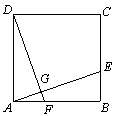
证明：在正方形ABCD中，∠DAF=∠ABE=90°， DA=AB
∵DG⊥AE， ∴∠FDA +∠DAG=90°
又∵∠EAB+∠DAG=90°， ∴∠FDA =∠EAB
∴△DAF≌△ABE
∴DF=AE
练习册系列答案
相关题目
已知：如图，边长为2的正五边形ABCDE内接于⊙O，AB、DC的延长线交于点F，过点E作EG∥CB交BA的延长线于点G．精英家教网
（1）求证：AB2=AG•BF；
（2）证明：EG与⊙O相切，并求AG、BF的长．
（2012•房山区一模）已知：如图，点P是线段AB上的动点，分别以AP、BP为边向线段AB的同侧作正△APC和正△BPD，AD和BC交于点M．
（1）当△APC和△BPD面积之和最小时，直接写出AP：PB的值和∠AMC的度数；
（2）将点P在线段AB上随意固定，再把△BPD按顺时针方向绕点P旋转一个角度α，当α＜60°时，旋转过程中，∠AMC的度数是否发生变化？证明你的结论．
（3）在第（2）小题给出的旋转过程中，若限定60°＜α＜120°，∠AMC的大小是否会发生变化？若变化，请写出∠AMC的度数变化范围；若不变化，请写出∠AMC的度数．
（1）已知：如图1，△ABC为正三角形，点M为BC边上任意一点，点N为CA边上任意一点，且BM=CN，BN与AM相交于Q点，试求∠BQM的度数．
（2）如果将（1）中的正三角形改为正方形ABCD（如图2），点M为BC上任意一点，点N为CD边上任意一点，且BM=CN，BN与AM相交于Q点，那么∠BQM等于多少度呢？说明理由．

（3）如果将（1）中的“正三角形”改为正五边形…正n边形（如图3），其余条件都不变，请你根据（1）、（2）的求解思路，将你推断的结论填入下表：（注：正多边形的各个角都相等）
正多边形 正五边形 … 正n边形
∠BQM的度数 …
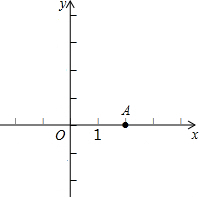（2013•浦东新区二模）已知：如图，点A（2，0），点B在y轴正半轴上，且OB=
1
2
OA，将点B绕点A顺时针方向旋转90°至点C．旋转前后的点B和点C都在抛物线y=-
5
6
x2+bx+c上，
（1）求点B、C的坐标；
（2）求该抛物线的表达式；
（3）联结AC，该抛物线上是否存在异于点B的点D，使点D与AC构成以AC为直角边的等腰直角三角形？如果存在，求出符合所有条件的D点坐标；如果不存在，请说明理由．
已知：如图，点D的坐标为（0，6），过原点O和点D点的圆交x轴的正半轴于A点，圆周角∠OCA=30°．
求（1）A点的坐标；
（2）图中阴影部分的面积．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网