题目内容
已知:如图,边长为2的正五边形ABCDE内接于⊙O,AB、DC的延长线交于点F,过点E作EG∥CB交BA的延长线于点G.
(1)求证:AB2=AG•BF;
(2)证明:EG与⊙O相切,并求AG、BF的长.
分析:欲证AB2=AG•BF,可证△EAG∽△FBC及正五边形ABCDE的特点得出;求AG、BF的长,需连接EF,易证明EF⊥BC,得出EF⊥EG,依据EG与⊙O相切,用切线的性质得出.
解答:证明:(1)易证五边形ABCDE的外角∠FCB=∠EAG=∠FBC,
∵EG∥CB,
∴∠EAG=∠FBC.
∴△EAG∽△FBC.
∴
=
,即BC•AE=AG•BF.
又∵BC=AE=AB,
∴AB2=AG•BF.①
(2)连接EF,由(1)可知FB=FC,即△FBC为等腰三角形,易知BA=CD,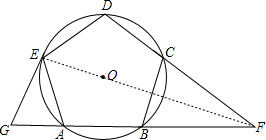
∴FA=FD,
∴EF⊥BC且EF平分BC,
∴EF过圆心O.
又∵EG∥CB,∴EF⊥EG,
∴EG与⊙O相切.
∴EG2=AG•BG.
由(1)可知∠G=∠EAG,∴EG=EA=2,
设AG=x,则22=x(x+2),解得x=
-1,
∴AG=
-1,代入①中可得:BF=
+1.
∵EG∥CB,
∴∠EAG=∠FBC.
∴△EAG∽△FBC.
∴
| AG |
| BC |
| AE |
| BF |
又∵BC=AE=AB,
∴AB2=AG•BF.①
(2)连接EF,由(1)可知FB=FC,即△FBC为等腰三角形,易知BA=CD,

∴FA=FD,
∴EF⊥BC且EF平分BC,
∴EF过圆心O.
又∵EG∥CB,∴EF⊥EG,
∴EG与⊙O相切.
∴EG2=AG•BG.
由(1)可知∠G=∠EAG,∴EG=EA=2,
设AG=x,则22=x(x+2),解得x=
| 5 |
∴AG=
| 5 |
| 5 |
点评:乘积的形式通常可以转化为比例的形式,通过相似三角形的性质得出,同时考查了切线的性质.

练习册系列答案
相关题目
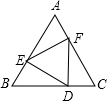 已知:如图,边长为a的正△ABC内有一边长为b的内接正△DEF,则△AEF的内切圆半径为
已知:如图,边长为a的正△ABC内有一边长为b的内接正△DEF,则△AEF的内切圆半径为 已知:如图,边长为2的圆内接正方形ABCD中,P为边CD的中点,直线AP交圆于E点.求弦DE的长及△PDE的面积.
已知:如图,边长为2的圆内接正方形ABCD中,P为边CD的中点,直线AP交圆于E点.求弦DE的长及△PDE的面积. (1997•南京)已知:如图,边长为2的等边三角形ABC,延长BC到D,使CD=BC,延长CB到E,使BE=CB,求△ADE的周长.
(1997•南京)已知:如图,边长为2的等边三角形ABC,延长BC到D,使CD=BC,延长CB到E,使BE=CB,求△ADE的周长.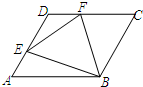 已知:如图,边长为a的菱形ABCD中,∠DAB=60°,E是异于A、D两点的动点,F是CD上的动点,请你判断:无论E、F怎样移动,当满足:AE+CF=a时,△BEF是什么三角形?并说明你的结论.
已知:如图,边长为a的菱形ABCD中,∠DAB=60°,E是异于A、D两点的动点,F是CD上的动点,请你判断:无论E、F怎样移动,当满足:AE+CF=a时,△BEF是什么三角形?并说明你的结论.