题目内容
 已知:如图,点D的坐标为(0,6),过原点O和点D点的圆交x轴的正半轴于A点,圆周角∠OCA=30°.
已知:如图,点D的坐标为(0,6),过原点O和点D点的圆交x轴的正半轴于A点,圆周角∠OCA=30°.求(1)A点的坐标;
(2)图中阴影部分的面积.
分析:(1)首先连接AD,由在同圆或等圆中,同弧或等弧所对的圆周角相等,即可求得∠ADO的度数,然后在Rt△AOD中,利用∠ADO的正切,即可求得OA的长,继而可得A点的坐标.
(2)从图中明确S阴=S扇形OBA-S△OBA,然后依公式计算即可.
(2)从图中明确S阴=S扇形OBA-S△OBA,然后依公式计算即可.
解答: 解:(1)连接AD.则∠ADO=∠OCA=30°,
解:(1)连接AD.则∠ADO=∠OCA=30°,
∵点D的坐标为(0,6),
∴OD=6,
在Rt△AOD中,OA=OD•tan∠ADO=6×
=2
,
∴A点的坐标为(2
,0).
(2)∵∠AOD=90°,
∴AD是该圆的直径,
过点O作AD边上的中线OB,则OB=AB=BD,即点B为该圆的圆心,
∴∠AOB=2∠OPCA=60°,
∴△OBA是等边三角形,
∴OB=AB=OA=2
.
∴S扇形OBA=
=2π,S△OBA=
×2
×2
×
=3
,
∴S阴=S扇形OBA-S△OBA=2π-3
.
 解:(1)连接AD.则∠ADO=∠OCA=30°,
解:(1)连接AD.则∠ADO=∠OCA=30°,∵点D的坐标为(0,6),
∴OD=6,
在Rt△AOD中,OA=OD•tan∠ADO=6×
| ||
| 3 |
| 3 |
∴A点的坐标为(2
| 3 |
(2)∵∠AOD=90°,
∴AD是该圆的直径,
过点O作AD边上的中线OB,则OB=AB=BD,即点B为该圆的圆心,
∴∠AOB=2∠OPCA=60°,
∴△OBA是等边三角形,
∴OB=AB=OA=2
| 3 |
∴S扇形OBA=
60π×(2
| ||
| 360 |
| 1 |
| 2 |
| 3 |
| 3 |
| ||
| 2 |
| 3 |
∴S阴=S扇形OBA-S△OBA=2π-3
| 3 |
点评:此题考查了圆周角定理与特殊角的三角函数.此题难度不大,解题的关键是掌握在同圆或等圆中,同弧或等弧所对的圆周角相等定理的应用,注意掌握辅助线的作法.

练习册系列答案
 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
相关题目
 已知,如图:点A(1,1),点B在坐轴上,试以OA为边,使三角形OAB为等腰三角形,试在图中画这个等腰三角形并求点B的坐标.
已知,如图:点A(1,1),点B在坐轴上,试以OA为边,使三角形OAB为等腰三角形,试在图中画这个等腰三角形并求点B的坐标.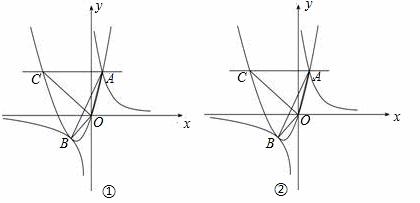
 经过A(2,0). 设顶点为点P,与x轴的另一交点为点B.
经过A(2,0). 设顶点为点P,与x轴的另一交点为点B. 上是否存在点D,使四边形OPBD为平行四边形?若存在,求出点D的坐
上是否存在点D,使四边形OPBD为平行四边形?若存在,求出点D的坐
 中,四边形OABC是矩形,点A,C的坐
中,四边形OABC是矩形,点A,C的坐 =-
=- +
+ 交折线O-A-B于点E.
交折线O-A-B于点E.

 已知,如图:点A(1,1),点B在坐轴上,试以OA为边,使三角形OAB为等腰三角形,试在图中画这个等腰三角形并求点B的坐标.
已知,如图:点A(1,1),点B在坐轴上,试以OA为边,使三角形OAB为等腰三角形,试在图中画这个等腰三角形并求点B的坐标.